Производная сложной функции - определение, формулы и примеры вычислений

Понятия и определения

Понятие производной основано на определении предела. Проще всего объяснить этот термин с помощью примера. Пусть существует определённое место, в которое можно попасть по нескольким дорогам. Эти пути разные, один из них прямой, другой - с подъёмами и спусками, третий идёт только в гору. Чтобы быстрее всего добраться до места, необходимо выбрать удобную дорогу, но для этого нужно знать местность.

Некоторый путь можно обозначить как y = f (n). Эта функция отображает рельеф местности, как бы вид пути сбоку. На одних интервалах кривая возрастает, а на других убывает. Максимальное значение функции находится в точке «А», а наименьшее в «В». Поэтому на промежутке от (- ɷ, а) график возрастает, а от (ɷ, b) убывает.

Взяв за дельта-эн приращение аргумента и прикладывая его к различным точкам функции, можно выявить следующую закономерность. Для любой точки в указанных промежутках можно подобрать такое значение дельта-эн, которое помещается в границах. А это означает, что отношение приращения по высоте будет всегда положительным в случае (Δy / Δn) > 0 и отрицательным, если (Δy / Δn) < 0. В том случае, когда отношение равно нулю, функция остаётся неизменной, то есть соответствует ровной дороге. Поэтому задача состоит в том, чтобы найти функцию, с помощью которой можно определить вид изменения.

Приняв, что приращение происходит в точке n0, можно записать Δy = f (n0+ Δn) — f (n0). Обозначив угол наклона через «а», можно выделить треугольник с углом «а». Согласно теореме, тангенс угла равен отношению противолежащего катета к прилежащему, то есть tg а = Δy/ Δn. Производной функцией в точке приращения n0 называют предел приращения Δy. Он зависит от аргумента Δn при значении n, стремящемся к нулю. Справедливо записать выражение:

f '(n0) = lim (f (n0 + Δn — f (n0)) / Δn, где предел лимита Δn стремится к нулю, но его не достигает (бесконечно мал).

Таким образом, производная функции основывается на понятии границы и непрерывности, характеризует скорость изменения. Определяется она пределом отношения приращения переменной к увеличению её аргумента при стремлении последнего к нулю. Если предел возможен, функция называется дифференцируемой. А сам процесс, по сути, является обратным интегрированию и называется дифференцированием.

Сложная функция

Вычисление производной функции f = f (n) выполняется по специальной таблице. Так, производная от числа равна нулю, поскольку скорость изменения постоянной равна нулю. Дифференциальное исчисление произведения числа на переменную n равна этому числу. Доказательство этой формулы простое. Существует четыре правила дифференцирования:

• Любую постоянную можно вынести за знак производной: p = (C*f (n))' = C*(f (n))'.
• Производная суммы или разности равняется сумме или разности каждой из них: (f (n) + g (n))' = (f (n))'+(g (n))' или (f (n) — g (n))' = (f (n))'-(g (n))'.
• При умножении двух функций производная равна их сумме: (f (n)*g (n))' = (f (n))'*g (n) + f (n)*(g (n))'.
• Производная функций дроби определяется отношением разности произведения знаменателя на дифференциал числителя и числителя на дифференциал знаменателя в квадрате: (f (n)/g (n)' = ((f (n)'*g (n) — f (n)*(g (n))') / (g (n))2.

Исходя из определений решением произведения будет (c*n)' = c*(n)' = c*1 = c. Таблица производных существует для степенных, прямых и обратных тригонометрических функций. Например, необходимо найти производную простой функции: y = (n)^½.

Согласно таблице производных, решением задачи будет 1/2 (n)^½. То есть ответ находится по определённым правилам. То же самое относится и к непростым функциям. Отличаются они от простых промежуточным элементом. Если принять, что s — функция от n, то s = s (n). Тогда запись y = f (s) будет представлять собой сложную функцию. В математике принято f называть внешней функцией, а s — внутренней.

Например, производная арктангенса сложной функции будет равна (arctg s)' = 1/(1+ s²)*s'. В специальной таблице указано 18 производных, начиная со степенного и кончая логарифмическим выражением. С её помощью и решаются такого рода задачи. Общую же, показательную, формулу для нахождения сложного изменения можно записать: (s (v (n)))' = s'(v) * v' (n), где s'(v) — внутреннее изменение, а v' (n) — внешнее.

Кроме всего, существует выражение вида y = eⁿ. Относится оно к простому виду и называется экспонентным. Запись же y = e^s считается уже сложной экспонентной, так как s = s (n).

Доказательство и теорема

Для того чтобы вычислить непростую функцию, необходимо знать теорему. Она гласит, что если s = ɷ (n) имеет производную s'n, а y = f (s) производную y' s, то сложное выражение y = f [ɷ (n)] в любой точке n можно найти по формуле: y'n = y's + s'n. Но более часто используют частное утверждение: производная сложного изменения находится как произведение рассматриваемой функции на промежуточный аргумент дифференциала.

Для доказательства теоремы нужно использовать приращения. Если для n оно будет определено как дельта-эн, то для s и y их приращения будут дельта-эс и дельта-игрек. Приняв, что когда дельта-эн стремится к нулю, а дельта-эс не имеет нулевых значений, можно записать тождество:

(Δy / Δn) = (Δy / Δs) * (Δs / Δn).

Используя предел, при котором дельта-эн стремится к нулю, получим:

lim (Δy / Δn) = lim ((Δy / Δs) * Δs / Δn)) = lim ((Δy / Δs) * ( Δs / Δn)).

Функция s = ɷ (n) дифференцируемая, а значит, непрерывная, поэтому при малых значения дельта-эн дельта-эс также будет стремиться к нулю. Следовательно, лимиты «эн» и «эс» равны. Поэтому будут верны и следующие записи:

• lim (Δy / Δn) = y'n, при дельта-эн, стремящимся к нулю;
• lim (Δs / Δn) = s'n, когда дельта-эн принимает малые величины;
• lim (Δy / Δs) = y's, при нулевых значениях дельта-эс.

Отсюда следует: y'n = y's + s'n, что и необходимо было доказать.

В большинстве задач математического анализа приходится сталкиваться с дифференцированием логарифмической функции. Эта зависимость представляется простой формулой: (ln n) = 1/n. Такое выражение получается из решения примеров натурального логарифма сложной функции. Производная, когда основанием является число «е», будет равна: (ln n)' = (log en)' = 1/(n * ln e) = 1/n. При этом используется свойство, что логарифм от числа с тем же самым основанием равен единице. Если же под натуральным логарифмом понимается s = s (n), то при дифференцировании логарифма правильно будет записать: (lns)' = (1/s) * s.

По аналогии выводится формула и для степенной функции вида у' = х^{sin n} . Такое выражение часто называют показательно-степенным. Определив логарифм двух частей, получим: ln y = ln nⁿ. Убрав показатель степени за скобку и учитывая, что y = y (n), можно записать:

• ln y = sin n * ln n;
• (ln y)' = (sin n * ln n)';
• (1/y) * y' = (sin n)' * ln n + ln (n)' * sin n;
• (1/y) * y' = cos n * ln n + sin n/n;
• y' = (cos n * ln n + sin n/n) * y.

Так как у = n^{sin n} , то решение будет следующим: y' = (cos n * ln n + sin n/n) * n ^{sin n}.

Примеры решения задач

Вычисление производных нашло широкое применение в решении физических задач и исследовании химических реакций. С помощью производной в физике рассчитывается ускорение и скорость распада радиоэлементов. Используя формулы, можно найти значение переменного тока и электродвижущую силу, наибольшую мощность. В химии производная помогает определить свойства веществ.

Но использование вычислений не ограничивается только техническими науками. Так, в географии дифференцирование даёт возможность рассчитать значения сейсмографии, изменение электромагнитного поля, провести полный анализ численности населения. В электротехнике - исследовать действие электрического тока, в экономике — окупаемость услуг и производительность труда.

Невозможно решить задачу без знания таблицы производных сложных функций. Для студентов существуют различные источники, из которых они могут получить нужную информацию. Это не только пособия по математическому анализу, но ещё и интернет-порталы. Существует множество онлайн-калькуляторов с подробным описанием решений. Например, kontrolnaya-rabota.ru, math. semestr.ru, allcalc.ru. Работают они практически все одинаково. Пользователю необходимо указать математическое выражение и переменную, а затем выбрать порядок производной, после чего запустить процесс и через несколько секунд получить результат с решением.

Нахождение квадратного корня

Нужно найти производную функцию подкоренного выражения y = 3-cos³ (ln(n+(n)^1/2)). Прежде всего необходимо разобраться во вложениях. Существует простой способ — мысленная замена «эн» на единицу и выполнение следующих шагов:

• Решение выражения (n+(n)^1/2). Подставив единицу, получим (1+(1)^1/2) = 2 – самое глубокое вложение.
• Расчёт логарифма: ln 2.
• Определение косинуса: cos (ln 2).
• Возведение косинуса в куб: cos³ (ln 2).
• Нахождение разности: 3 – cos³ (ln 2).
• Решение квадратного корня: (3-cos³(ln 2))^1/2.

Формула дифференцирования непростой функции: (s(v))’ = u’(v)*v’, используется в обратном порядке. Решение будет следующим:

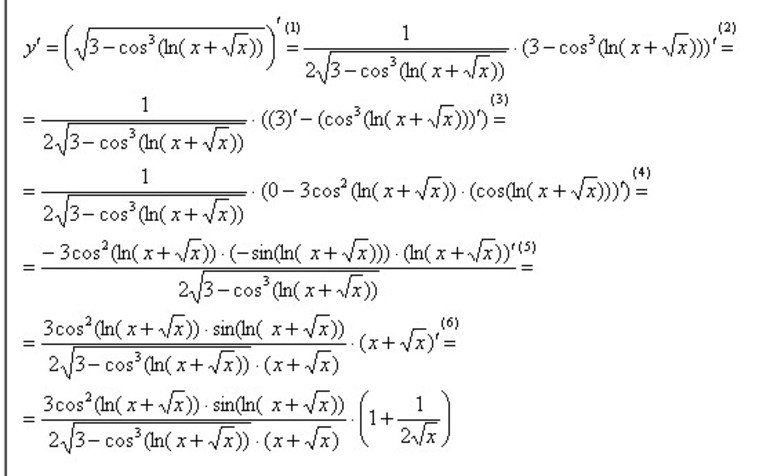
При решении сначала берут производную от квадратного корня. Затем разности и степени куба. Теперь останется определить дифференциал от косинуса и логарифма. На последнем этапе вычисляют самое глубокое вложение.

Производная арктангенса

При нахождении арктангенса также опираются на таблицу производных и теорему. Например, необходимо вычислить функцию y ’ = 18 * arctg²⁴ (8 * ln n). Согласно правилам нахождения, постоянное число можно вынести за пределы знака производной. Поэтому функцию можно упростить до вида:

y ′ = 18 * (arctg²⁴ (8 * ln n))′.

Чтобы найти нужное выражение из таблицы, задачу следует представить в стандартной записи: (arctg (8 * ln n))²⁴ . Подставив в формулу (s^α) ′ = α * s^{α − 1} * s’ рассматриваемый пример, получим: s = arctg (8 * ln n) , где α = 12 . Выбирать нужно именно эту формулу, так как внешняя функция находится впереди.

Исходя из полученного равенство можно представить записью: y ′ = (18 * arctg²⁴ (8 * ln n))′ = 18 * (arctg²⁴ (8 * ln n))′ = 432 * (arctg (8 * ln n))²² * (arctg (8 * ln n))′ . Возведение в степень 24 является внешней функцией, поэтому именно с неё начинается нахождение производной.

На следующем шаге ищется производная (arctg (8 * ln n ))′. Подставив в формулу находимое выражение, получим следующее равенство :

(arctg (8 * ln n))′ = (1 / (1 + (8 * ln n)²) * (8 * ln n)′.

Учитывая, что (8 * ln n)² = 64 * (ln n)² = 16 ⋅ ln² n, выражение можно упростить:

(arctg (8 * ln n))′ = 1/((1 + ( 8 * ln n )² * 8 * ln n)′) = 1 /(( 1 + 16 * ln 2n) * (4 * ln n)′). Отсюда рассматриваемое равенство можно преобразовать:

y′ = (18 * arctg²⁴ (8 * ln n))′ = 18 * (arctg²⁴ (8 * ln n))′.

Выражение снова можно упростить: y ′ = 432 * (arctg (8 * ln n))²² * (arctg (4 * ln n))′ и переписать в более наглядном виде: y′ = 432 * (arctg (8 * ln n)) ²² * 1/(1 + 64 ⋅ ln ² n * (8 * ln n)’.

Осталось вычислить (8 * ln n)′. Константа переносится за знак производной. Используя выражение u = n / (ln n) ′ = (1 / n) * n′, получим: (ln n)′ = (1 / n) * n ′ = (1 / n)* 1 = 1 / n.

Теперь следует подставить выражение в общую формулу:

y′ = (18 * arctg²⁴ (8 * ln n)) ′ = 432 * (arctg (8 * ln n))²² * (1/ (1 + 64 * ln² n )) * (4 * ln n)’.

= 432 * arctg²² (4 * ln n) n * (1 + 16 * ln 2 n).

Упростив выражение, получим: y ′ = 432 * (arctg²² (4 * ln n)) / (n * (1 + 64 * ln²n), что и является ответом на поставленную задачу.

Таким образом, решение дифференциалов непростых функций выполнить несложно. Главное — знать таблицу производных и правильно выделять в ней элементарные составляющие.