Выделение полного квадрата - формулы, методы и примеры решений

Однако не все его знают. В результате этого объем вычислений увеличивается, а также допускаются ошибки. Он также применяется для нахождения корней уравнений и построения графиков.
Общая информация
Выделить полный квадрат из многочлена второй степени означает, что его следует привести к более читабельной формуле. Эта операция применяется в следующих случаях: интегрирование, дифференцирование, построение графиков и решение уравнений (чаще — в последних двух).
За основу взяты три формулы сокращенного умножения (разложение квадратного многочлена на множители), которые специалисты рекомендуют запомнить или выписать отдельно.
К ним относятся следующие соотношения:
- Квадрат суммы: (y + z)^2 = y 2 + 2yz + z 2 .
- Квадрат разности: (y — z)^2 = y 2 — 2yz + z 2 .
- Разность квадратов: y 2 — z 2 = (y — z)(y + z).
Существует правило, позволяющее выполнить операцию упрощения многочлена ay 2 + by + c второй степени путем разложения его на множители. Это означает, что его следует свести (преобразовать) к виду a * (y — y0)^2 + y0.
Универсальный алгоритм
Алгоритмом называется комплексное решение, состоящее из последовательного набора правил. Преобразование ay 2 + by + c осуществляется следующим образом:

- Привести к такому виду первое слагаемое на основании формулы (y + z)^2 = y 2 + 2yz + z 2 : [(a)^(½) * y]^2. Корень из коэффициента «а» следует указывать обязательно.
- Второе слагаемое должно состоять из удвоенного произведения: by = [(2 * (a)^(½) * y)] * (b / [2 * (a)^(½)].
- Третий свободный член находится по формуле z = (b / [2 * (a)^(½)].
- Для равновесия следует отнять число, полученное в пункте 3.
- Записать результат нужно таким образом: [(a)^(½) * y]^2 + [(2 * (a)^(½) * y)] * (b / [2 * (a)^(½)] + [(b / (2 * (a)^(½))]^2 — [(b / (2 * (a)^(½))]^2 + c.
Для квадрата разности алгоритм похожий. Формула выделения полного квадрата имеет такой вид: [(a)^(½) * y]^2 — [(2 * (a)^(½) * y)] * (b / [2 * (a)^(½)] + [(b / (2 * (a)^(½))]^2 — [(b / (2 * (a)^(½))]^2 + c. Соотношение также применяется математиками в алгебре, а также в различных дисциплинах с физико-математическим уклоном. Для этого нужно воспользоваться таким подробным объяснением правил решения:
- Запись формулы: ay 2 — c = ((a)^(½) * y — (c)^(½))((a)^(½) * y + (c)^(½)).
- Коэффициент «с^(½)» должен быть равен целому числу.
- Если условие во втором пункте не выполняется, то следует воспользоваться таким соотношением: с + a — a= с1 — a.
- Записать выражение в таком виде: ay 2 — c + a — a = ((a)^(½) * y — (c1)^(½))((a)^(½) * y + (c1)^(½)) — a.
Число «а» может быть положительным или отрицательным. Если его прибавить к «с», то должно получиться значение «с1».
При извлечении квадратного корня результат должен быть целым. Чтобы равенство не нарушалось, следует прибавить и отнять «а».
Алгоритм записан в общем виде. В теории он является сложным для понимания.
Однако при практическом применении некоторые неясности исчезают. Для начала нужно разобрать, где его нужно применять.
Сферы использования
Математики рекомендуют разобрать основные примеры выделения полного квадрата. Следует их систематизировать, поскольку это позволит оптимизировать процесс решения. Основной смысл заключается в применении соответствующих алгоритмов для экономии времени.
Некоторые считают, что шаблонами пользоваться нежелательно. Однако в этом есть и свои положительные стороны. Например, при поступлении в какое-либо высшее учебное заведение следует придерживаться общепринятых вариантов решения. При успешном зачислении в университет можно применить нестандартные подходы выполнения задания.

Шаблоны широко применяются не только в дисциплинах с физико-математическим уклоном, но и в программировании.
Распространенными заданиями с упрощением квадратного трехчлена являются:
- построение графиков квадратичной функции;
- решение уравнений;
- упрощение выражений.
Для нахождения решений следует подробно разобрать алгоритмы. Нет необходимости заучивать основные определения, формулы и правила. Их следует понимать, поскольку в философии есть такой закон: «переход количества в качество». Кроме того, программистами были созданы специальные онлайн-калькуляторы, позволяющие получить полный квадрат, разложить многочлен на множители и так далее.
Построение графиков
Графиком квадратичной функции z = a[y — c]^2 + d является кривая, которая называется параболой. Далее следует ввести следующие пояснения:
- Коэффициенты «а» и «с» — некоторые числа. Последнее вычисляется по такой формуле: с = b / 2a.
- Константа «d» является свободным членом.
Следует отметить, что расположение графика функции зависит от вышеописанных коэффициентов. Для построения параболы математики рекомендуют разобрать частные случаи:
- Направление ветвей: вверх (a > 0) и вниз (a < 0).
- Смещение вершины на величину «с»: по оси ОУ в положительную сторону (c > 0), по ОУ в отрицательном направлении (c < 0) и находится на ОХ (c = 0).
- Смещение по ОХ: в сторону положительных значений на (b / 2a) и отрицательных — (-b / 2a).
Уравнение параболы всегда нужно приводить к правильному виду, поскольку график будет строить намного проще. Кроме того, его можно построить, зная частные случаи, и схематически.
Нахождение корней
Решить квадратное уравнение вида az 2 + bz + с = 0 означает найти все его корни или доказать, что их нет. Его можно решать несколькими методами: нахождение дискриминанта, использование теоремы Виета или представление в виде квадрата.
При использовании первого метода нужно воспользоваться таким алгоритмом:

- Упростить выражение (выведение общего множителя, раскрытие скобок и приведение подобных слагаемых).
- Вычисление дискриминанта: D = (-b)^2 — 4ac.
- Разобрать частные случаи, и выбрать ход решения, который зависит от значения D: при D > 0 решением уравнения являются два значения или корня (z1 = -b — D^(½) / 2a и z2 = -b + D^(½) / 2a; D = 0 — один корень (z = -b / 2a) и D < 0 — нет корней.
- Подставить корни, полученные при решении, и проверить уравнение — значение в левой части должно быть равно нулю (0 = 0).
Вид квадратного уравнения зависит от коэффициентов a, b и c. Если а = 0, то старшая степень исчезает, и тождество превращается в обыкновенное линейное равенство (bz + c = 0) или функцию, графиком которой является прямая, а не парабола. При а = 1 его можно решить при помощи второго способа, который называется теоремой Виета (z1 + z2 = - b и z1 * z2 = с). Когда b = 0 (az 2 + c = 0), то дискриминант можно не высчитывать. Решение находится следующим образом:
- Нужно перенести свободный член «с» в правую сторону. Если с < 0, то решений нет. Когда значения c > 0, необходимо перейти ко второму шагу решения.
- Разделить обе части на «а».
- Вычислить корни по формулам (будут одинаковыми числами, но с разными знаками): z1 = -[c/a]^(½) z2 = [c/a]^(½).
Когда коэффициент с = 0 (az 2 + bz = 0), то решить уравнение очень просто.

Для этого нужно произвести такие действия:
- Сократить обе части на «a».
- Вынести за скобку общий множитель: z (z + b/a) = 0.
- Решить два уравнения: z1 = 0 и z2 + b/a = 0.
- Проверить корни, подставив в исходное тождество.
Третий способ — выделение квадрата или использование формул сокращенного умножения. В этом случае нет необходимости использовать стандартный первый метод. Если построить график функции, то корнями будут являться его точки пересечения с осью абсцисс. Можно получить решения при помощи математических преобразований. Последний считается менее точным способом, поскольку корнями могут быть иррациональные числа, а не действительные.
Упрощение выражений
Бывают случаи, когда следует решить уравнение, упростив его. Например, чтобы решить равенство (2z 2 — 5z + 7) + (z + 5)(z + 3) = 0, нужно раскрыть скобки, а затем привести подобные слагаемые. Этот способ называется методом математических преобразований.
В некоторых случаях следует возвести в квадрат, а затем привести подобные слагаемые. После этого необходимо опять воспользоваться формулами, сгруппировав элементы.
Этот шаг позволяет оптимизировать процесс вычислений. Например, нет необходимости подставлять численные значения в выражение z 2 + 4z + 16 + z 2 — 16. Его можно просто упростить: z 2 + 8z + 16 + z 2 — 16 = (z + 4)^2 + (z — 4)(z + 4) = (z + 4)(z + 4 + z — 4) = 2z (z + 4).
Пример решения
Необходимо решить квадратное уравнение z^2 + 20z + 50 = 6z + 5 несколькими способами, используя следующие методы: нахождение дискриминанта, формул разложения, теоремы Виета и построить график. Вычисление корней первым методом (через дискриминант) выглядит таким образом:

- Упростить выражение: z^2 + 20z + 50 - 6z - 5 = z^2 + 14z + 45.
- Вычислить дискриминант: D = 14^2 - 4 * 1 * 45 = 196 - 180 = 16 = 4^2.
- Осуществить анализ второго пункта: если D = 16 > 0, то значит у уравнения два корня.
- Первый корень: z1 = (-14 - 4) / 2 = -9.
- Второе решение: z2 = (-14 + 4) / 2 = -5.
- Проверка: (-9)^2 + (-9) * 14 + 45 = 81 - 126 + 45 = 0 и (-5)^2 + (-5) * 14 + 45 = 25 - 70 + 45 = 0.
Два корня подходят, поскольку равенство 0 = 0 соблюдается. Специалисты рекомендуют опускать проверку, поскольку задача решается несколькими способами.
Второй метод заключается в использовании теоремы Виета. Произвести поиск корней довольно просто, поскольку а = 1. Воспользовавшись формулами z1 + z2 = - 14 и z1 * z2 = 45, можно подобрать корни: z1 = -9 и z2 = -5.
Третий метод заключается в использовании формул разложения. Их разрешается применять несколько раз и в любом порядке. Алгоритм решения выглядит таким образом:

- Разложить на множители (формула квадрат суммы): z^2 + 14z + 45 = z^2 + 14z + 45 + 4 - 4 = (z^2 + 14z + 49) - 4 = (z + 7)^2 - 4.
- Использовать формулу разности квадратов двух чисел: (z + 7)^2 - 4 = (z + 7 - 2)(z + 7 - 2) = (z + 5)(z + 9).
- Записать в виде уравнений: (z + 5) = 0 и (z + 9) = 0.
- Корни: z1 = -5 и z2 = -9.
Использование графического метода позволит получить точные значения, поскольку во всех предыдущих способах они являются целыми числами. Необходимо записать уравнения параболы (можно воспользоваться вторым пунктом алгоритма третьего метода): (z + 7)^2 - 4. Анализ перед построением выглядит таким образом:
- Ветви направлены вверх, поскольку a = 1 > 0.
- Смещение вершины по ОУ на -4 в отрицательном направлении (с < 0), а по ОХ — на 7.
Для построения следует составить таблицу 1 зависимости функции y от аргумента z. По значениям также можно вычислить корни (все y = 0).
| y | 0 | -3 | 0 | 5 | 21 | 45 | 77 | 117 | 165 |
| z | -9 | -6 | -5 | -4 | -2 | 0 | 2 | 4 | 6 |
Таблица 1. Подготовка к построению.
После подготовки необходимо строить график. Это можно выполнить ручным методом или воспользоваться специализированным сайтом. Последним рекомендуется пользоваться только при проверке правильности решения.
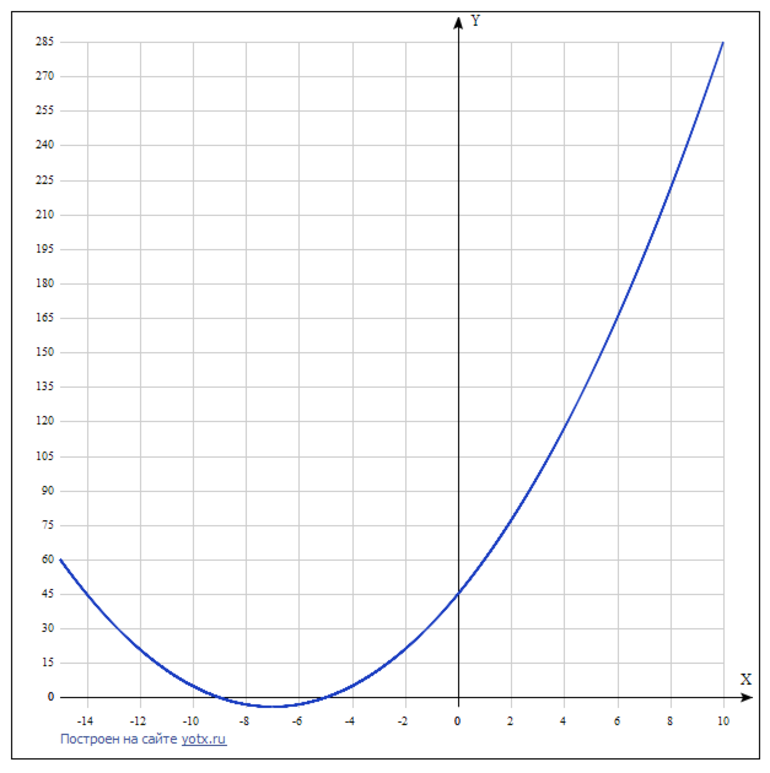
Рисунок 1. Графическое представление y = z^2 + 14 * z + 45.
На графике видно, что корнями уравнения являются числа -9 и -5. Они совпадают с полученными ранее значениями. Следовательно, решение является верным. Числа можно также подставить в исходное равенство.
Таким образом, при решении уравнений, упрощении выражений и построении графиков функций рекомендуется применять формулы сокращенного умножения. Это позволит сохранить много времени.
Все тесты
- Биология
- История
- Сочинения
- Пунктуация
- Фонетический разбор
- Пушкин А.С
- Религия
- Карьера
- Информатика
- Физика
- Стихи
- Математика
- Обществознание
- ОБЖ
- Окружающий мир
- Экономика
- Биографии
- Анализ стихотворений
- Русский язык
- Краткие содержания
- Физкультура
- Орфография
- География
- Помощь студенту
- Литература
- Подготовка к ЕГЭ
- Тест на тему Что такое “железное легкое” и как жилось узникам аппарата 5 вопросов
- Тест на тему Суть и методы клеточной инженерии 5 вопросов
- Тест на тему Злаковые растения - общая характеристика, признаки и список представителей 7 вопросов
- Тест на тему Семейство бобовые - общая характеристика, строение и представители 7 вопросов
- Тест на тему Суть “дела Дрейфуса” и реакция общества 5 вопросов
- Тест на тему Деятельность партии монтаньяров во Франции 5 вопросов
- Тест на тему Традиции и обычаи украинского народа 5 вопросов
- Тест на тему Причины закрытия Японии в 17 веке и последствия 5 вопросов
- Тест на тему Подготовка и содержание генерального плана “Ост” 5 вопросов
- Тест на тему Тайны убийства Петра Столыпина 5 вопросов
- Тест на тему Отмена подушной подати на Руси 5 вопросов
- Тест на тему Период регентства Елены Глинской: события и реформы 5 вопросов
- Тест на тему Экономика России в годы Первой мировой войны 5 вопросов
- Тест на тему Битва при деревне Лесной 28 сентября 1708 года 5 вопросов
- Тест на тему 10 любопытных фактов про Рождество 5 вопросов
- Тест на тему 10 любопытных фактов про Новый год 5 вопросов
- Тест на тему История потешных полков Петра Первого 5 вопросов
- Тест на тему Образование и распад тушинского лагеря при Лжедмитрии II 5 вопросов
- Тест на тему Чем ведал и какие функции выполнял Разрядный приказ? 5 вопросов
- Тест на тему Задачи и направления внешней политики России в 16 веке 5 вопросов
- Тест на тему Установление и отмена бессрочного сыска беглых крестьян на Руси 5 вопросов
- Тест на тему История создания и деятельности Вольного экономического общества 5 вопросов
- Тест на тему Период правления Вещего Олега: внешняя и внутренняя политика 5 вопросов
- Тест на тему Правление и политика князя Игоря 5 вопросов
- Тест на тему Суть и последствия Нерчинского договора России с Китаем 1689 года 5 вопросов
- Тест на тему Причины, ход и итоги войны за польское наследство 1733-1735 гг. 5 вопросов
- Тест на тему Восстановление экономики СССР после Великой Отечественной Войны 5 вопросов
- Тест на тему Как и зачем были созданы полки иноземного строя 5 вопросов
- Тест на тему Создание стрелецких войск при Иване Грозном 5 вопросов
- Тест на тему Причины, ход событий и итоги выступления старообрядцев при Петре I 7 вопросов
- Тест на тему Как и почему началась Ливонская война: основные причины 5 вопросов
- Тест на тему К чему привела опричнина Ивана Грозного: последствия для страны 5 вопросов
- Тест на тему Положение черносошных крестьян на Руси 5 вопросов
- Тест на тему История Астраханского восстания: причины, события, итоги 7 вопросов
- Тест на тему Деятельность Великого посольства Петра I 5 вопросов
- Тест на тему Герои отечественной войны 1812 года - характеристика участников и полководцев 5 вопросов
- Тест на тему Развитие системы образования и науки в первой половине 19 века 6 вопросов
- Тест на тему Первые князья Киевской Руси - даты правления и особенности проводимой политики 7 вопросов
- Тест на тему Характеристика, периоды развития жизни в Палеозойскй эре 7 вопросов
- Тест на тему История праздника 23 февраля - происхождение и значение для России 7 вопросов
- Тест на тему Кто придумал отмечать 8 марта: история праздника 8 вопросов
- Тест на тему Славянские праздники - список праздников, обрядов и обычаев славян 10 вопросов
- Тест на тему Образ Шарикова в повести «Собачье сердце» М. Булгакова 5 вопросов
- Тест на тему Образы героев в повести «Невский проспект» Н. Гоголя 5 вопросов
- Тест на тему Московские главы в романе «Мастер и Маргарита» Булгакова 7 вопросов
- Тест на тему Описание образа бирюка из рассказа И. Тургенева 7 вопросов
- Тест на тему Образы героев в романе «Отцы и дети» И. Тургенева 7 вопросов
- Тест на тему Образы героев в повести «Котлован» А. Платонова 7 вопросов
- Тест на тему Образы героев в пьесе «Гроза» А. Островского 7 вопросов
- Тест на тему История создания повести Н. В. Гоголя “Шинель” 7 вопросов
- Тест на тему История создания сборника рассказов Тургенева “Записки охотника” 7 вопросов
- Тест на тему История создания повести "Муму" Ивана Тургенева 7 вопросов
- Тест на тему История создания стихотворения "Реквием" Анны Ахматовой 10 вопросов
- Тест на тему История создания повести Гоголя "Тарас Бульба" 10 вопросов
- Тест на тему История создания стихотворения Пушкина "Деревня" 6 вопросов
- Тест на тему История создания стихотворения М. Лермонтова “Нищий” 7 вопросов
- Тест на тему История создания стихотворения "Она сидела на полу" 7 вопросов
- Тест на тему История создания Пушкиным стихотворения "К морю" 6 вопросов
- Тест на тему История создания повести «Станционный смотритель» А. Пушкина 10 вопросов
- Тест на тему История создания «Оды на день восшествия» М. Ломоносова 7 вопросов
- Тест на тему "Банты" - как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Конечно же» - выделяется ли слово запятыми? 5 вопросов
- Тест на тему «Подчеркивать» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Лифты» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Строку» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Апостроф» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Зубчатый» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Прозорлива» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Балашиха» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Реку» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Полно» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Говорено» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Досыта» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Упрочение» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Развила» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Подолгу» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Логин» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Окон» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Втридорога» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Утра» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Запломбированный» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Цыган» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Шарфы» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Бармен» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Положенный» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Крадущийся» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Донизу» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Явишься» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Ободрить» - как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Предприняв» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Прочтено» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Низок» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Исчерпать» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Роба» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Исчерпывающий» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Будучи» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Понятым» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Повторен» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Изредка» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Донельзя» − как ставить ударение в слове? 5 вопросов
- Тест на тему «Загодя» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Принужден» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Опошлить» − как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Краны» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Торты» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Инструмент» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Брало» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Забрала» − как правильно ставить ударение? 5 вопросов
- Тест на тему «Отзыв» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Рефлексия» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему Как люди узнают о том, что было в прошлом? 5 вопросов
- Тест на тему Какие животные впадают в спячку зимой: объяснения зоологов 7 вопросов
- Тест на тему Сообщение по окружающему миру для 4 класса об острове Врангеля 5 вопросов
- Тест на тему Сообщение о морских обитателях - описание, виды и названия 7 вопросов
- Тест на тему Биография поэта и писателя Льва Рубинштейна 5 вопросов
- Тест на тему Биография президента Белоруссии Александра Лукашенко 5 вопросов
- Тест на тему 10 интересных фактов про Афанасия Фета 5 вопросов
- Тест на тему 10 интересных фактов про Ивана Тургенева 5 вопросов
- Тест на тему Биография писателя и поэта Вячеслава Урюпина 5 вопросов
- Тест на тему Биография поэта Николая Михайловича Рубцова 5 вопросов
- Тест на тему Биография поэта Андрея Дмитриевича Дементьева 5 вопросов
- Тест на тему Биография президента РФ Владимира Путина 5 вопросов
- Тест на тему Биография и личная жизнь Даниила Хармса 5 вопросов
- Тест на тему Краткая биография Валентины Осеевой 5 вопросов
- Тест на тему Григорий Остер: биография писателя и избранные произведения 7 вопросов
- Тест на тему Елена Благинина: творческая биография и личная жизнь 10 вопросов
- Тест на тему Биография детской писательницы Ирины Пивоваровой 5 вопросов
- Тест на тему Анализ стихотворения «Догорел апрельский светлый вечер…» И. Бунина 5 вопросов
- Тест на тему Анализ стихотворения «Фонтан» Ф. Тютчева 5 вопросов
- Тест на тему Анализ стихотворения «Посмотри - какая мгла» Я. Полонского 5 вопросов
- Тест на тему Анализ стихотворения «Школьник» Н. Некрасова 5 вопросов
- Тест на тему Анализ стихотворения «Несжатая полоса» Н. Некрасова 5 вопросов
- Тест на тему «Весенний дождь» - анализ стихотворения А.А. Фета 7 вопросов
- Тест на тему «Поет зима - аукает» - анализ стихотворения С.А. Есенина 7 вопросов
- Тест на тему Сообщение на тему: «Традиции русской речевой манеры общения» 5 вопросов
- Тест на тему Определение и виды простых осложненных предложений 5 вопросов
- Тест на тему Какие бывают виды текстов? 5 вопросов
- Тест на тему Образование и правописание страдательных причастий настоящего времени 5 вопросов
- Тест на тему Как определить начальную форму прилагательного? 5 вопросов
- Тест на тему Местоимение-прилагательное в русском языке 5 вопросов
- Тест на тему Сборник правил по русскому языку для 6 класса 7 вопросов
- Тест на тему Сборник правил по русскому языку за 5 класс 7 вопросов
- Тест на тему Упражнения для тренировки школьников 7 класса по причастному обороту 9 вопросов
- Тест на тему Тест: Склонение фамилий в русском языке 7 вопросов
- Тест на тему Общеупотребительные и необщеупотребительные слова 5 вопросов
- Тест на тему Дефисное и слитное написание сложных прилагательных 5 вопросов
- Тест на тему Морфологический разбор числительного - правило и примеры 5 вопросов
- Тест на тему «Акула» Л. Толстого - краткое содержание 5 вопросов
- Тест на тему Русская народная сказка «Хвосты» - краткое содержание 5 вопросов
- Тест на тему Краткое содержание оперы «Снегурочка» Римского-Корсакова 5 вопросов
- Тест на тему «Обезьяний язык» М. Зощенко – краткое содержание 10 вопросов
- Тест на тему «Сердце не камень» - краткое содержание пьесы А.Н. Островского 5 вопросов
- Тест на тему Балет «Щелкунчик» — краткое содержание 7 вопросов
- Тест на тему Реферат по физкультуре на тему: «Здоровое питание» 5 вопросов
- Тест на тему История развития лыжного спорта в разных странах - классификация и интересные факты 6 вопросов
- Тест на тему Важность самоконтроля при занятиях спортом 5 вопросов
- Тест на тему Как выполняются прыжки через козла? 5 вопросов
- Тест на тему Что такое здоровый образ жизни? 5 вопросов
- Тест на тему Как правильно выполнять кувырки? 5 вопросов
- Тест на тему Развитие гибкости тела: упражнения и польза для тела 5 вопросов
- Тест на тему Виды и польза прыжков через скакалку 5 вопросов
- Тест на тему Какие есть зимние виды спорта? 5 вопросов
- Тест на тему Реферат на тему: “Гимнастика как вид спорта” 8 вопросов
- Тест на тему Реферат по физкультуре на тему “Футбол” 7 вопросов
- Тест на тему Реферат по физкультуре на тему: “Баскетбол - виды и лиги” 7 вопросов
- Тест на тему Реферат на тему «Лыжный спорт» 10 вопросов
- Тест на тему Реферат по физической культуре «Формы и виды закаливания» 10 вопросов
- Тест на тему Правописание слов с непроверяемой безударной гласной в корне 5 вопросов
- Тест на тему Нужно ли ставить запятую к фразе - "с уважением"? 5 вопросов
- Тест на тему «Во-вторых» или «во вторых» – как правильно пишется? 5 вопросов
- Тест на тему "Нету" или "нет" - как правильно писать и говорить? 5 вопросов
- Тест на тему «Не я» или «нея» – как правильно пишется? 5 вопросов
- Тест на тему «Полным-полно» или «полным полно» - как правильно пишется? 5 вопросов
- Тест на тему Как пишется «кто-нибудь» или «кто нибудь»? 5 вопросов
- Тест на тему Мягкий знак после шипящих в глаголах - правила, примеры 5 вопросов
- Тест на тему «Потвёрже» или «по твёрже» – как правильно пишется? 5 вопросов
- Тест на тему «Какой-то» или «какой то» – как пишется правильно? 5 вопросов
- Тест на тему «Мало-помалу» или «мало помалу» – как правильно пишется? 5 вопросов
- Тест на тему «По-осеннему» или «по осеннему» – как правильно пишется? 5 вопросов
- Тест на тему "Находу" или "на ходу" - слитно или раздельно писать? 5 вопросов
- Тест на тему "ЮлИчка" или "ЮлЕчка" - как правильно писать? 5 вопросов
- Тест на тему «Не пойму» или «непойму» – как правильно пишется? 5 вопросов
- Тест на тему «Доброе утро» − как правильно пишется? 5 вопросов
- Тест на тему «Почему-то» или «почему то» – как правильно пишется? 5 вопросов
- Тест на тему «На вынос» или «навынос» – как правильно пишется? 5 вопросов
- Тест на тему «Невежливо» или «не вежливо» – как правильно пишется? 5 вопросов
- Тест на тему «Негодуя» или «не годуя» - как правильно пишется? 5 вопросов
- Тест на тему «КуриНый» или «куриННый» − как правильно пишется? 5 вопросов
- Тест на тему «ТеННис» или «теНис» – как правильно пишется? 5 вопросов
- Тест на тему «ТумаННый» или «тумаНый» – как правильно пишется? 5 вопросов
- Тест на тему «ЗамечеННый» или «замечеНый» – как правильно пишется? 5 вопросов
- Тест на тему «Семнадцать» или «семЬнадцать» – как правильно пишется? 5 вопросов
- Тест на тему «ВыздОравливающий» или «выздАравливающий» – как правильно пишется? 5 вопросов
- Тест на тему «Свеж» или «свежЬ» – как правильно пишется? 5 вопросов
- Тест на тему «СлаЩе» или «слаДЧе» – как правильно пишется? 5 вопросов
- Тест на тему «ПрЕтерпевать» или «прИтерпевать» - как правильно пишется? 5 вопросов
- Тест на тему «Удастся» или «удастЬся» – как правильно пишется? 5 вопросов
- Тест на тему «СписаНо» или «СписаННо» – как правильно пишется? 5 вопросов
- Тест на тему «Происшествие» или «проишествие» – как правильно пишется? 5 вопросов
- Тест на тему «НачИнающий» или «начЕнающий» – как правильно пишется? 5 вопросов
- Тест на тему «Невозможно» или «не возможно» – как пишется слитно или раздельно? 5 вопросов
- Тест на тему «Налету» или «на лету» – как правильно пишется? 5 вопросов
- Тест на тему «Надолго» или «на долго» – как правильно пишется? 5 вопросов
- Тест на тему «ПьющАя» или «пьющЕя» – как правильно пишется? 5 вопросов
- Тест на тему «Неужели» или «не ужели» − как правильно пишется? 5 вопросов
- Тест на тему «НИкого» или «нЕкого» – как правильно пишется? 5 вопросов
- Тест на тему «БаССейн» или «баСейн» − как правильно пишется? 5 вопросов
- Тест на тему "Не согласованно" или "несогласованно" - слитно или раздельно? 5 вопросов
- Тест на тему «ОбстОятельствам» или «обстАятельствам» – как правильно пишется? 5 вопросов
- Тест на тему «ОбижеННый» или «обижеНый» – как правильно пишется? 5 вопросов
- Тест на тему «Аллах» или «Алах» – как правильно пишется? 5 вопросов
- Тест на тему «БелОрусский» или «белАрусский» – как правильно пишется? 5 вопросов
- Тест на тему «ЧИсло» или «чЕсло» – как правильно пишется? 5 вопросов
- Тест на тему «УвЕряющий» или «увИряющий» – как правильно пишется? 5 вопросов
- Тест на тему «НенасТный» или «ненасный» – как правильно пишется? 5 вопросов
- Тест на тему «Постричь» или «поДстричь» – как правильно пишется? 5 вопросов
- Тест на тему «КоЛея» или «коЛЛея» – как правильно пишется? 5 вопросов
- Тест на тему Характеристика природных зон Поволжья 5 вопросов
- Тест на тему Для каких рек в России характерно летнее половодье? 5 вопросов
- Тест на тему Как правильно заполнять дневник наблюдения за погодой 5 вопросов
- Тест на тему Влажные экваториальные леса - особенности климата, характеристика флоры и фауны 7 вопросов
- Тест на тему Европейский север России - географическое положение, особенности развития предприятий и промышленности 7 вопросов
- Тест на тему Что такое масштаб карты и как его определять 7 вопросов
- Тест на тему Особенности и примеры островных государств 5 вопросов
- Тест на тему Природные зоны Южной Америки - характеристики и особенности 7 вопросов
- Тест на тему 10 интересных фактов про океан 7 вопросов
- Тест на тему Сектор Газа: где он находится и откуда такое название? 6 вопросов
- Тест на тему Что нужно сдавать на бухгалтера? 5 вопросов
- Тест на тему Какие предметы нужно сдавать на пилота 5 вопросов
- Тест на тему Какие экзамены нужно сдавать на фотографа? 5 вопросов
- Тест на тему Какие предметы нужно сдавать на хореографа? 5 вопросов
- Тест на тему Какие предметы нужно сдавать на актера? 5 вопросов
- Тест на тему Какие предметы нужно сдавать на режиссера? 5 вопросов
- Тест на тему Что нужно сдавать на художника? 5 вопросов
- Тест на тему Что нужно сдавать для поступления на визажиста? 5 вопросов
- Тест на тему Какие экзамены нужно сдавать на полицейского? 5 вопросов
- Тест на тему Какие предметы нужно сдавать на фармацевта? 5 вопросов
- Тест на тему Какие предметы сдавать для поступления на врача? 5 вопросов
- Тест на тему Какие экзамены нужно сдавать на учителя 5 вопросов
- Тест на тему Кадетский корпус - как поступить, чему учат и условия для проживания 5 вопросов
- Тест на тему Готовы ли вы к поступлению на психолога? 5 вопросов
- Тест на тему Готовы ли вы к поступлению на дизайнера? 5 вопросов
- Тест на тему Какие экзамены нужно сдавать на стюардессу? 5 вопросов
- Тест на тему Какие экзамены нужно сдавать на повара? 5 вопросов
- Тест на тему Какие предметы сдавать для поступления на программиста 5 вопросов
- Тест на тему Готовы ли вы сдавать экзамены на стоматолога? 5 вопросов
- Тест на тему Готовы ли вы сдавать экзамены на маркетолога? 5 вопросов
- Тест на тему Готовы ли вы сдавать экзамены на ветеринара? 5 вопросов
- Тест на тему Готовы ли вы поступать на экономиста? 5 вопросов
- Тест на тему Готовы ли вы к поступлению на юриста? 5 вопросов
- Тест на тему Готовы ли вы поступать на архитектора? 5 вопросов
- Тест на тему Характеристика Дуняши в романе “Тихий Дон” М. Шолохова 5 вопросов
- Тест на тему Описание образа Фамусова - персонажа комедии “Горе от ума” 5 вопросов
- Тест на тему Характеристика образа Сатина - персонажа пьесы “На дне” М. Горького 5 вопросов
- Тест на тему Анализ повести “Сашка” В. Кондратьева 5 вопросов
- Тест на тему Характеристика образа Фауста из трагедии Гёте 9 вопросов
- Тест на тему Анализ романа “Портрет Дориана Грея” О. Уайльда 5 вопросов
- Тест на тему Характеристика колобка - героя русской народной сказки 5 вопросов
- Тест на тему Образ главной героини “Алисы в стране чудес” Л. Кэррола 5 вопросов
- Тест на тему Трактовки образа Иисуса Христа в поэме “Двенадцать” А. Блока 5 вопросов
- Тест на тему Образ Настеньки из повести “Белые ночи” Ф. Достоевского 5 вопросов
- Тест на тему Конфликт в рассказе “После бала” Л. Толстого 5 вопросов
- Тест на тему Образ главной героини повести “Бедная Лиза” Н. Карамзина 5 вопросов
- Тест на тему Описание образа Васютки из рассказа “Васюткино озеро” В. Астафьева 5 вопросов
- Тест на тему Образы чиновников в комедии “Ревизор” Н. Гоголя 5 вопросов
- Тест на тему Роль образа вишневого сада в пьесе А. Чехова 5 вопросов
- Тест на тему Характеристика профессора Преображенского в повести “Собачье сердце” М. Булгакова 5 вопросов
- Тест на тему Описание образа городничего в комедии “Ревизор” Н. Гоголя 5 вопросов
- Тест на тему Описание образа главного героя “Доктора Живаго” Б. Пастернака 5 вопросов
- Тест на тему Образ Цыганка в повести “Детство” М. Горького 5 вопросов
- Тест на тему Характеристика Вани Солнцева в повести “Сын полка” В. Катаева 5 вопросов
- Тест на тему Образ автора в поэме "Василий Теркин" А. Твардовского 5 вопросов
- Тест на тему Образ портрета в повести "Портрет" Н. В. Гоголя 5 вопросов
- Тест на тему Описание образа девушки-ундины из “Героя нашего времени” М. Лермонтова 5 вопросов
- Тест на тему Описание образа Натальи Савишной в повести “Детство” Л. Толстого 5 вопросов
- Тест на тему Описание образа Костылина из “Кавказского пленника”. Л. Толстого 5 вопросов
- Тест на тему Описание образа Карла Ивановича в повести “Детство” Л. Толстого 5 вопросов
- Тест на тему Описание образа Жилина в “Кавказском пленнике” Л. Толстого 5 вопросов
- Тест на тему Описание образа Дины из “Кавказского пленника” Л. Толстого 5 вопросов
- Тест на тему Описание образа Вулича из “Героя нашего времени” М. Лермонтова 5 вопросов
- Тест на тему Описание образов татар в “Кавказском пленнике” Л. Толстого 5 вопросов
- Тест на тему Описание образа профессора Пирогова в рассказе “Чудесный доктор” А. Куприна 5 вопросов
- Тест на тему Народные образы героев в сказе «Серебряное копытце» П. Бажова 5 вопросов
- Тест на тему Описание образа Акакия Акакиевича Башмачкина из “Шинели” Н. Гоголя 5 вопросов
- Тест на тему Описание образов Лели и Миньки в одноименном рассказе М. Зощенко 5 вопросов
- Тест на тему Описание образа Сотникова из повести “Сотников” В. Быкова 5 вопросов
- Тест на тему Описание образов родителей в повести “Детство” Л. Толстого 5 вопросов
- Тест на тему Описание образа Флягина в “Очарованном страннике” Н. Лескова 5 вопросов
- Тест на тему Анализ комедии «Мещанин во дворянстве» Мольера 5 вопросов
- Тест на тему Описание образов героев рассказа “Галоша” М. Зощенко 5 вопросов
- Тест на тему Образ полковника - отца Вареньки из рассказа “После бала” Л. Толстого 5 вопросов
- Тест на тему Образ шинели в повести Н. В. Гоголя "Шинель" 5 вопросов
- Тест на тему Биография поэта Алексея Васильевича Кольцова 5 вопросов
- Тест на тему «Вечный зов» А. Иванова - краткое содержание 5 вопросов
- Тест на тему «Убийство в восточном экспрессе» А. Кристи - краткое содержание 5 вопросов
- Тест на тему Образ бабушки в повести «Детство» М. Горького 5 вопросов
- Тест на тему Описание образа барыни в рассказе «Муму» И. Тургенева 5 вопросов
- Тест на тему Главные произведения, написанные Александром Блоком 5 вопросов
- Тест на тему История создания песни “В лесу родилась елочка” 5 вопросов
- Тест на тему История создания поэмы “Двенадцать” А. Блока 5 вопросов
- Тест на тему История создания повести “Белые ночи” Ф. Достоевского 5 вопросов
- Тест на тему Аргументы к сочинению на тему: «Добро и зло в пьесе “Гроза” А. Островского» 5 вопросов
- Тест на тему Аргументы к сочинению 15.3 из пьесы «Горе от ума» 5 вопросов
- Тест на тему Аргументы к итоговому сочинению по рассказу «Матренин двор» А. Солженицына 5 вопросов
- Тест на тему Аргументы для итогового сочинения ЕГЭ по роману «Мастер и Маргарита» 5 вопросов
- Тест на тему Аргументы к итоговому сочинению по рассказу «Куст сирени» 5 вопросов
- Тест на тему Аргументы для итогового сочинения ЕГЭ по «Гарри Поттеру» 5 вопросов







