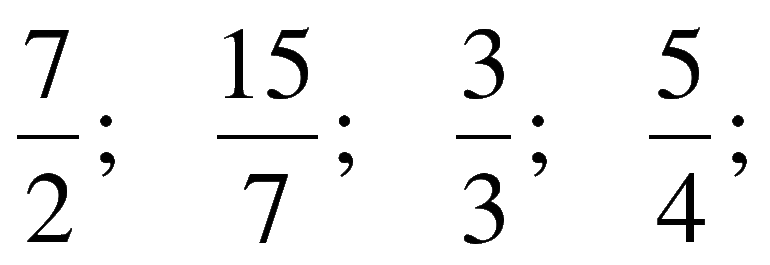Рациональные дроби - свойства, преобразования и примеры решений
Общие сведения
Математика — наука о числах и действиях над ними. Значение, которое можно записать в виде обыкновенной дроби, называют рациональным. Оно состоит из целого числа в числителе и натурального в знаменателе. Простое выражение можно представить как бесконечную десятичную дробь. Множество рациональных чисел обозначают латинской буквой Q. Если действительное значение не рациональное, оно иррациональное.
Рациональные дроби — это конструкции над многочленами. Это следует из того, что делимое и делитель представляют собой сумму нескольких одночленов. Если в выражении стоит знак минус, на него не стоит обращать внимание, ведь он относится к числовому коэффициенту одночлена, поэтому многочлен всё равно является суммой. Например, -4/d2 * (b — c), (f + 2,67 * f + 2 3/8 — f2 * y* t)/(f2 + d2 +42).
Выражения могут быть представлены в нестандартном виде, поэтому приходится выполнять дополнительные преобразования. Это возможно, так как делимое и делитель являются самодостаточными. Упрощения выполняются путём разложения на множители. При этом по возможности следует выполнять действия как для числителя, так и знаменателя. Операции преобразования включают в себя:
- сокращение;
- приведение к общему знаменателю и нахождению дополнительных членов;
- вынесение общего множителя за скобку.
Наиболее часто вызывает сложность подбор общего знаменателя. Это приведение основывается на основном свойстве дроби. Согласно ему, умножение на ненулевой многочлен одновременно делимого и делителя не приводит к изменению результата. Отсюда следует, что числитель и знаменатель можно возводить в квадрат, извлекать корень.
Для успешного выполнения действий важно знать формулы сокращённого умножения. Это базисные знания, без которых решать рациональные дроби в 8 классе будет невозможно.
Всего используется 7 теорем: разность кубов и квадратов, произведение разности и суммы, куб суммы и разности, умножение на неполный квадрат. Используя знания, полученные в седьмом классе, многие операции можно выполнять в уме и приводить многочлен к стандартному виду без предварительного раскрытия скобок.
Свойства дроби
Пусть имеется множество, каждому члену которого поставлено в соответствие число игрек. Про такое положение говорят, что множеству задана числовая функция: y = f (x), где x Є D. Описывается область определением функции и обозначается как D (f (x)). Множество можно представить как отношение двух многочленов. Когда в числителе стоит многочлен энной степени, а в знаменателе эмной, то f (x) называют рациональным отношением или дробью.
Такие выражения обладают рядом свойств. Основное из них выражают формулой: P (x)/Q (x) = P (x) * R (x) / Q (x) * R (x). Справедливо оно лишь для случая, при котором множества Q (x) и R (x) неравны нулю, при этом R (x) является многочленом. Формулировка свойства звучит следующим образом: делимое и делитель можно помножить на одинаковое выражение. Например, им может быть число, одночлен или другой многочлен.
К другим свойствам относят:
- ассоциативность;
- коммутативность;
- дистрибутивность;
- транзитивность.
Если равенство f/g =y/x справедливо, при этом y/x = n/m, верным будет и выражение: f/g = n/m. Отсюда следует, что рациональную дробь можно превратить в обыкновенную, если её делитель и делимое можно умножить или разделить на одинаковый многочлен. Единственное условие — он должен быть отличным от нуля.
Рациональную дробь можно представить в виде суммы. Выполняют это действие, основываясь на правиле сложения или вычитания выражений с одинаковыми знаменателями. Например, k * m — k / k+1 = 1/k + (k2 * m — k2 — k — 1) / (k2 + k).
Из свойств рациональных отношений следует, что для вычитания их друг из друга нужно привести члены к общему знаменателю и найти разность числителей. Аналогично поступают и для операции сложения, только вычитание в числителе заменяют складыванием. Произведение же находится простым перемножением делимых и делителей. А вот деление выполняют по-другому. Чтобы найти частное, нужно первое выражение умножить на обратную вторую дробь. Чтобы возвести дробь в степень, нужно отдельно в неё возвести числитель и знаменатель. По тому же принципу извлекают и корень.
Понимая, как правильно использовать приведённые свойства, решать задания на контрольной работе в школе будет несложно. Но перед сдачей теста необходимо попрактиковаться в самостоятельном решении.
Изменение знака
При решении заданий основное свойство дроби используют и для изменения знаков. Действительно, если числитель и знаменатель помножить на минус единицу, ответ не изменится. Полученное выражение будет полностью тождественным исходному. Записать это правило можно равенством: a/b = (-1 * a) / (-1 * b) = -a/-b. Например, (-23x — 34) / (x — y) = (23x + 34) / (y — x).
Из теоремы существует следствие. Согласно ему, a / b = - (-a) / b = - (a) / (-b). Доказать это утверждение просто если взять за основу правило умножения чисел. Дробь — (-a) / b = -((-a): b) = (-1) * (((-1) * a): b) = (-1) * (-1) * a: b = a: b = a / b. Аналогичные действия можно выполнить и для равенства: a / b = - (a) / (-b).
Правило изменения знаков очень важно, поэтому обычно ему уделяют целый урок при изучении рациональных дробей и их свойств в 8 классе. Понять, насколько полезно это свойство можно, рассмотрев пример. Найти сумму рациональных чисел: ((3 — 14x) / (3x * y — z)) + ((14 — 56x) / (z -3x * y)). Чтобы сложить два члена, нужно найти общий знаменатель. Применяя стандартные методы, вычислить его довольно сложно. Решение получится громоздким и неудобным. Если же присмотреться к выражениям, можно увидеть похожесть знаменателей, отличие их будет только в знаках.
Используя правило изменения, можно умножить второй член на минус единицу, то есть помножить на -1 делитель и делимое: -1 * (14 — 56x) / -1* (z -3x * y). В результате получится дробь тождественная исходной: (-14 + 56x) / (-z + 3x * y) = (56x — 14) / (3x * y — z). Теперь полученный результат можно подставить в пример и выполнить сложение: ((3 — 14x) / (3x * y — z)) + (56x — 14) / (3x * y — z) = ((3 — 14x) + (56x — 14)) / (3x * y — z) = ((3 — 14) + (56x — 14x)) / (3x * y — z) = (44x -11) / (3x * y — z).
Следует отметить, что приём по изменению знака часто используют при разложении рациональных отношений на простейшие дроби. Например, (2x3 — 3) / (- x3 — x). Так как степень числа в числителе меньше чем в знаменателе, нужно использовать разложение. Причём в другом случае пришлось бы применять деление для нахождения целой части. Для удобства действия выражение нужно умножить на минус единицу. В результате несложно будет определить верность равенства: 2x3 + 3 / (x3 + x) = 2 + (-2x + 3) / (x3 + x).
Решение примеров
Самостоятельное решение рациональных дробей в алгебре в 8 классе строится на цепочке преобразований. Первое, что нужно сделать — оценить возможность разложения отношения на множители. Для этого лучше использовать формулы сокращённого умножения или дискриминант. Алгоритм преобразований можно представить в следующем виде:
- подобрать формулу сокращённого умножения, то есть перевести выражение в максимально возможную степень;
- вынести общую степень за скобку;
- при существовании коэффициентов найти их по формуле квадратного разложения.
Вот 3 типовые задачи, которые обычно предлагают решить студентам при сдаче зачёта:
- Используя свойства дробных отношений, выполнить преобразование до стандартного вида: (3 *a — a*b — 2*b*(5/6)*b + 2 3/7*a*b) / (a3*b2 — 5*a2*b + 3*a**b -15). Оценивая пример, можно увидеть, что к числителю возможно применить свойство степени из-за одинаковых оснований: 3*a — a*b — 2*b*(5/6)*b + 2 3/7*a*b = 3*a — a*b — (5/3)*b2 + 2 3/7*a*b. В полученном выражении подобный член можно убрать за скобки: 3*a + (-a*b + 2 3/7*a*b) — 5/3*b2 = 3*a + 1 3/7 *a*b — 5/3*b2. Теперь можно перейти к разложению знаменателя. В нём общий множитель вынести за скобки. В результате должно получиться выражение: a*b*(a2*b + 3) — 5*(a2*b + 3) = (a2*b + 13)*(a*b -5). Осталось только записать полученные результаты в числитель и знаменатель.
- Сократить дробь: (45z*x2*y3) / (45z*x*y7). Сразу видно, что числитель и знаменатель содержит одинаковый множитель, на который можно сократить. Затем, применив свойство степени, выражение можно представить в следующем виде: x2*y3 / x*y7 = (x*x)*y3 / x*(y3*y4) = x/y4.
- Определить, при каких значениях n рациональная дробь (n4 — 2 * n3 + 4 * n — 5) / (n-2) будет равняться целому числу. Для решения задачи нужно выполнить деление. Для этого удобно воспользоваться методом столбика. После преобразования дробь должна принять вид: n3 + 4 + 3/(n-2). Так как n3 + 4 при любом значении неизвестной будет целым, анализировать нужно дробь: 3/(n-2). Она будет целой, только если знаменатель будет равняться: 1, −1, 3, -3. Соответственно искомые значения равняются: 3;1;5;1.
При упрощении рациональных отношений сложность связана с тем, что не всегда просто найти общий множитель для числителя и знаменателя. Причём он и не всегда существует, поэтому и нужно пробовать разложение на множители. Если такого члена нет, дробь упростить нельзя.
Все тесты
- Биология
- История
- Сочинения
- Пунктуация
- Фонетический разбор
- Пушкин А.С
- Религия
- Карьера
- Информатика
- Физика
- Стихи
- Математика
- Обществознание
- ОБЖ
- Окружающий мир
- Экономика
- Биографии
- Анализ стихотворений
- Русский язык
- Краткие содержания
- Физкультура
- Орфография
- География
- Помощь студенту
- Литература
- Подготовка к ЕГЭ
- Тест на тему Что такое “железное легкое” и как жилось узникам аппарата 5 вопросов
- Тест на тему Суть и методы клеточной инженерии 5 вопросов
- Тест на тему Злаковые растения - общая характеристика, признаки и список представителей 7 вопросов
- Тест на тему Семейство бобовые - общая характеристика, строение и представители 7 вопросов
- Тест на тему Суть “дела Дрейфуса” и реакция общества 5 вопросов
- Тест на тему Деятельность партии монтаньяров во Франции 5 вопросов
- Тест на тему Традиции и обычаи украинского народа 5 вопросов
- Тест на тему Причины закрытия Японии в 17 веке и последствия 5 вопросов
- Тест на тему Подготовка и содержание генерального плана “Ост” 5 вопросов
- Тест на тему Тайны убийства Петра Столыпина 5 вопросов
- Тест на тему Отмена подушной подати на Руси 5 вопросов
- Тест на тему Период регентства Елены Глинской: события и реформы 5 вопросов
- Тест на тему Экономика России в годы Первой мировой войны 5 вопросов
- Тест на тему Битва при деревне Лесной 28 сентября 1708 года 5 вопросов
- Тест на тему 10 любопытных фактов про Рождество 5 вопросов
- Тест на тему 10 любопытных фактов про Новый год 5 вопросов
- Тест на тему История потешных полков Петра Первого 5 вопросов
- Тест на тему Образование и распад тушинского лагеря при Лжедмитрии II 5 вопросов
- Тест на тему Чем ведал и какие функции выполнял Разрядный приказ? 5 вопросов
- Тест на тему Задачи и направления внешней политики России в 16 веке 5 вопросов
- Тест на тему Установление и отмена бессрочного сыска беглых крестьян на Руси 5 вопросов
- Тест на тему История создания и деятельности Вольного экономического общества 5 вопросов
- Тест на тему Период правления Вещего Олега: внешняя и внутренняя политика 5 вопросов
- Тест на тему Правление и политика князя Игоря 5 вопросов
- Тест на тему Суть и последствия Нерчинского договора России с Китаем 1689 года 5 вопросов
- Тест на тему Причины, ход и итоги войны за польское наследство 1733-1735 гг. 5 вопросов
- Тест на тему Восстановление экономики СССР после Великой Отечественной Войны 5 вопросов
- Тест на тему Как и зачем были созданы полки иноземного строя 5 вопросов
- Тест на тему Создание стрелецких войск при Иване Грозном 5 вопросов
- Тест на тему Причины, ход событий и итоги выступления старообрядцев при Петре I 7 вопросов
- Тест на тему Как и почему началась Ливонская война: основные причины 5 вопросов
- Тест на тему К чему привела опричнина Ивана Грозного: последствия для страны 5 вопросов
- Тест на тему Положение черносошных крестьян на Руси 5 вопросов
- Тест на тему История Астраханского восстания: причины, события, итоги 7 вопросов
- Тест на тему Деятельность Великого посольства Петра I 5 вопросов
- Тест на тему Герои отечественной войны 1812 года - характеристика участников и полководцев 5 вопросов
- Тест на тему Развитие системы образования и науки в первой половине 19 века 6 вопросов
- Тест на тему Первые князья Киевской Руси - даты правления и особенности проводимой политики 7 вопросов
- Тест на тему Характеристика, периоды развития жизни в Палеозойскй эре 7 вопросов
- Тест на тему История праздника 23 февраля - происхождение и значение для России 7 вопросов
- Тест на тему Кто придумал отмечать 8 марта: история праздника 8 вопросов
- Тест на тему Славянские праздники - список праздников, обрядов и обычаев славян 10 вопросов
- Тест на тему Образ Шарикова в повести «Собачье сердце» М. Булгакова 5 вопросов
- Тест на тему Образы героев в повести «Невский проспект» Н. Гоголя 5 вопросов
- Тест на тему Московские главы в романе «Мастер и Маргарита» Булгакова 7 вопросов
- Тест на тему Описание образа бирюка из рассказа И. Тургенева 7 вопросов
- Тест на тему Образы героев в романе «Отцы и дети» И. Тургенева 7 вопросов
- Тест на тему Образы героев в повести «Котлован» А. Платонова 7 вопросов
- Тест на тему Образы героев в пьесе «Гроза» А. Островского 7 вопросов
- Тест на тему История создания повести Н. В. Гоголя “Шинель” 7 вопросов
- Тест на тему История создания сборника рассказов Тургенева “Записки охотника” 7 вопросов
- Тест на тему История создания повести "Муму" Ивана Тургенева 7 вопросов
- Тест на тему История создания стихотворения "Реквием" Анны Ахматовой 10 вопросов
- Тест на тему История создания повести Гоголя "Тарас Бульба" 10 вопросов
- Тест на тему История создания стихотворения Пушкина "Деревня" 6 вопросов
- Тест на тему История создания стихотворения М. Лермонтова “Нищий” 7 вопросов
- Тест на тему История создания стихотворения "Она сидела на полу" 7 вопросов
- Тест на тему История создания Пушкиным стихотворения "К морю" 6 вопросов
- Тест на тему История создания повести «Станционный смотритель» А. Пушкина 10 вопросов
- Тест на тему История создания «Оды на день восшествия» М. Ломоносова 7 вопросов
- Тест на тему "Банты" - как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Конечно же» - выделяется ли слово запятыми? 5 вопросов
- Тест на тему «Подчеркивать» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Лифты» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Строку» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Апостроф» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Зубчатый» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Прозорлива» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Балашиха» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Реку» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Полно» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Говорено» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Досыта» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Упрочение» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Развила» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Подолгу» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Логин» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Окон» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Втридорога» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Утра» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Запломбированный» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Цыган» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Шарфы» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Бармен» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Положенный» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Крадущийся» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Донизу» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Явишься» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Ободрить» - как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Предприняв» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Прочтено» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Низок» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Исчерпать» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Роба» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Исчерпывающий» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Будучи» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Понятым» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Повторен» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Изредка» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Донельзя» − как ставить ударение в слове? 5 вопросов
- Тест на тему «Загодя» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Принужден» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Опошлить» − как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Краны» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Торты» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Инструмент» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Брало» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Забрала» − как правильно ставить ударение? 5 вопросов
- Тест на тему «Отзыв» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Рефлексия» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему Как люди узнают о том, что было в прошлом? 5 вопросов
- Тест на тему Какие животные впадают в спячку зимой: объяснения зоологов 7 вопросов
- Тест на тему Сообщение по окружающему миру для 4 класса об острове Врангеля 5 вопросов
- Тест на тему Сообщение о морских обитателях - описание, виды и названия 7 вопросов
- Тест на тему Биография поэта и писателя Льва Рубинштейна 5 вопросов
- Тест на тему Биография президента Белоруссии Александра Лукашенко 5 вопросов
- Тест на тему 10 интересных фактов про Афанасия Фета 5 вопросов
- Тест на тему 10 интересных фактов про Ивана Тургенева 5 вопросов
- Тест на тему Биография писателя и поэта Вячеслава Урюпина 5 вопросов
- Тест на тему Биография поэта Николая Михайловича Рубцова 5 вопросов
- Тест на тему Биография поэта Андрея Дмитриевича Дементьева 5 вопросов
- Тест на тему Биография президента РФ Владимира Путина 5 вопросов
- Тест на тему Биография и личная жизнь Даниила Хармса 5 вопросов
- Тест на тему Краткая биография Валентины Осеевой 5 вопросов
- Тест на тему Григорий Остер: биография писателя и избранные произведения 7 вопросов
- Тест на тему Елена Благинина: творческая биография и личная жизнь 10 вопросов
- Тест на тему Биография детской писательницы Ирины Пивоваровой 5 вопросов
- Тест на тему Анализ стихотворения «Догорел апрельский светлый вечер…» И. Бунина 5 вопросов
- Тест на тему Анализ стихотворения «Фонтан» Ф. Тютчева 5 вопросов
- Тест на тему Анализ стихотворения «Посмотри - какая мгла» Я. Полонского 5 вопросов
- Тест на тему Анализ стихотворения «Школьник» Н. Некрасова 5 вопросов
- Тест на тему Анализ стихотворения «Несжатая полоса» Н. Некрасова 5 вопросов
- Тест на тему «Весенний дождь» - анализ стихотворения А.А. Фета 7 вопросов
- Тест на тему «Поет зима - аукает» - анализ стихотворения С.А. Есенина 7 вопросов
- Тест на тему Сообщение на тему: «Традиции русской речевой манеры общения» 5 вопросов
- Тест на тему Определение и виды простых осложненных предложений 5 вопросов
- Тест на тему Какие бывают виды текстов? 5 вопросов
- Тест на тему Образование и правописание страдательных причастий настоящего времени 5 вопросов
- Тест на тему Как определить начальную форму прилагательного? 5 вопросов
- Тест на тему Местоимение-прилагательное в русском языке 5 вопросов
- Тест на тему Сборник правил по русскому языку для 6 класса 7 вопросов
- Тест на тему Сборник правил по русскому языку за 5 класс 7 вопросов
- Тест на тему Упражнения для тренировки школьников 7 класса по причастному обороту 9 вопросов
- Тест на тему Тест: Склонение фамилий в русском языке 7 вопросов
- Тест на тему Общеупотребительные и необщеупотребительные слова 5 вопросов
- Тест на тему Дефисное и слитное написание сложных прилагательных 5 вопросов
- Тест на тему Морфологический разбор числительного - правило и примеры 5 вопросов
- Тест на тему «Акула» Л. Толстого - краткое содержание 5 вопросов
- Тест на тему Русская народная сказка «Хвосты» - краткое содержание 5 вопросов
- Тест на тему Краткое содержание оперы «Снегурочка» Римского-Корсакова 5 вопросов
- Тест на тему «Обезьяний язык» М. Зощенко – краткое содержание 10 вопросов
- Тест на тему «Сердце не камень» - краткое содержание пьесы А.Н. Островского 5 вопросов
- Тест на тему Балет «Щелкунчик» — краткое содержание 7 вопросов
- Тест на тему Реферат по физкультуре на тему: «Здоровое питание» 5 вопросов
- Тест на тему История развития лыжного спорта в разных странах - классификация и интересные факты 6 вопросов
- Тест на тему Важность самоконтроля при занятиях спортом 5 вопросов
- Тест на тему Как выполняются прыжки через козла? 5 вопросов
- Тест на тему Что такое здоровый образ жизни? 5 вопросов
- Тест на тему Как правильно выполнять кувырки? 5 вопросов
- Тест на тему Развитие гибкости тела: упражнения и польза для тела 5 вопросов
- Тест на тему Виды и польза прыжков через скакалку 5 вопросов
- Тест на тему Какие есть зимние виды спорта? 5 вопросов
- Тест на тему Реферат на тему: “Гимнастика как вид спорта” 8 вопросов
- Тест на тему Реферат по физкультуре на тему “Футбол” 7 вопросов
- Тест на тему Реферат по физкультуре на тему: “Баскетбол - виды и лиги” 7 вопросов
- Тест на тему Реферат на тему «Лыжный спорт» 10 вопросов
- Тест на тему Реферат по физической культуре «Формы и виды закаливания» 10 вопросов
- Тест на тему Правописание слов с непроверяемой безударной гласной в корне 5 вопросов
- Тест на тему Нужно ли ставить запятую к фразе - "с уважением"? 5 вопросов
- Тест на тему «Во-вторых» или «во вторых» – как правильно пишется? 5 вопросов
- Тест на тему "Нету" или "нет" - как правильно писать и говорить? 5 вопросов
- Тест на тему «Не я» или «нея» – как правильно пишется? 5 вопросов
- Тест на тему «Полным-полно» или «полным полно» - как правильно пишется? 5 вопросов
- Тест на тему Как пишется «кто-нибудь» или «кто нибудь»? 5 вопросов
- Тест на тему Мягкий знак после шипящих в глаголах - правила, примеры 5 вопросов
- Тест на тему «Потвёрже» или «по твёрже» – как правильно пишется? 5 вопросов
- Тест на тему «Какой-то» или «какой то» – как пишется правильно? 5 вопросов
- Тест на тему «Мало-помалу» или «мало помалу» – как правильно пишется? 5 вопросов
- Тест на тему «По-осеннему» или «по осеннему» – как правильно пишется? 5 вопросов
- Тест на тему "Находу" или "на ходу" - слитно или раздельно писать? 5 вопросов
- Тест на тему "ЮлИчка" или "ЮлЕчка" - как правильно писать? 5 вопросов
- Тест на тему «Не пойму» или «непойму» – как правильно пишется? 5 вопросов
- Тест на тему «Доброе утро» − как правильно пишется? 5 вопросов
- Тест на тему «Почему-то» или «почему то» – как правильно пишется? 5 вопросов
- Тест на тему «На вынос» или «навынос» – как правильно пишется? 5 вопросов
- Тест на тему «Невежливо» или «не вежливо» – как правильно пишется? 5 вопросов
- Тест на тему «Негодуя» или «не годуя» - как правильно пишется? 5 вопросов
- Тест на тему «КуриНый» или «куриННый» − как правильно пишется? 5 вопросов
- Тест на тему «ТеННис» или «теНис» – как правильно пишется? 5 вопросов
- Тест на тему «ТумаННый» или «тумаНый» – как правильно пишется? 5 вопросов
- Тест на тему «ЗамечеННый» или «замечеНый» – как правильно пишется? 5 вопросов
- Тест на тему «Семнадцать» или «семЬнадцать» – как правильно пишется? 5 вопросов
- Тест на тему «ВыздОравливающий» или «выздАравливающий» – как правильно пишется? 5 вопросов
- Тест на тему «Свеж» или «свежЬ» – как правильно пишется? 5 вопросов
- Тест на тему «СлаЩе» или «слаДЧе» – как правильно пишется? 5 вопросов
- Тест на тему «ПрЕтерпевать» или «прИтерпевать» - как правильно пишется? 5 вопросов
- Тест на тему «Удастся» или «удастЬся» – как правильно пишется? 5 вопросов
- Тест на тему «СписаНо» или «СписаННо» – как правильно пишется? 5 вопросов
- Тест на тему «Происшествие» или «проишествие» – как правильно пишется? 5 вопросов
- Тест на тему «НачИнающий» или «начЕнающий» – как правильно пишется? 5 вопросов
- Тест на тему «Невозможно» или «не возможно» – как пишется слитно или раздельно? 5 вопросов
- Тест на тему «Налету» или «на лету» – как правильно пишется? 5 вопросов
- Тест на тему «Надолго» или «на долго» – как правильно пишется? 5 вопросов
- Тест на тему «ПьющАя» или «пьющЕя» – как правильно пишется? 5 вопросов
- Тест на тему «Неужели» или «не ужели» − как правильно пишется? 5 вопросов
- Тест на тему «НИкого» или «нЕкого» – как правильно пишется? 5 вопросов
- Тест на тему «БаССейн» или «баСейн» − как правильно пишется? 5 вопросов
- Тест на тему "Не согласованно" или "несогласованно" - слитно или раздельно? 5 вопросов
- Тест на тему «ОбстОятельствам» или «обстАятельствам» – как правильно пишется? 5 вопросов
- Тест на тему «ОбижеННый» или «обижеНый» – как правильно пишется? 5 вопросов
- Тест на тему «Аллах» или «Алах» – как правильно пишется? 5 вопросов
- Тест на тему «БелОрусский» или «белАрусский» – как правильно пишется? 5 вопросов
- Тест на тему «ЧИсло» или «чЕсло» – как правильно пишется? 5 вопросов
- Тест на тему «УвЕряющий» или «увИряющий» – как правильно пишется? 5 вопросов
- Тест на тему «НенасТный» или «ненасный» – как правильно пишется? 5 вопросов
- Тест на тему «Постричь» или «поДстричь» – как правильно пишется? 5 вопросов
- Тест на тему «КоЛея» или «коЛЛея» – как правильно пишется? 5 вопросов
- Тест на тему Характеристика природных зон Поволжья 5 вопросов
- Тест на тему Для каких рек в России характерно летнее половодье? 5 вопросов
- Тест на тему Как правильно заполнять дневник наблюдения за погодой 5 вопросов
- Тест на тему Влажные экваториальные леса - особенности климата, характеристика флоры и фауны 7 вопросов
- Тест на тему Европейский север России - географическое положение, особенности развития предприятий и промышленности 7 вопросов
- Тест на тему Что такое масштаб карты и как его определять 7 вопросов
- Тест на тему Особенности и примеры островных государств 5 вопросов
- Тест на тему Природные зоны Южной Америки - характеристики и особенности 7 вопросов
- Тест на тему 10 интересных фактов про океан 7 вопросов
- Тест на тему Сектор Газа: где он находится и откуда такое название? 6 вопросов
- Тест на тему Что нужно сдавать на бухгалтера? 5 вопросов
- Тест на тему Какие предметы нужно сдавать на пилота 5 вопросов
- Тест на тему Какие экзамены нужно сдавать на фотографа? 5 вопросов
- Тест на тему Какие предметы нужно сдавать на хореографа? 5 вопросов
- Тест на тему Какие предметы нужно сдавать на актера? 5 вопросов
- Тест на тему Какие предметы нужно сдавать на режиссера? 5 вопросов
- Тест на тему Что нужно сдавать на художника? 5 вопросов
- Тест на тему Что нужно сдавать для поступления на визажиста? 5 вопросов
- Тест на тему Какие экзамены нужно сдавать на полицейского? 5 вопросов
- Тест на тему Какие предметы нужно сдавать на фармацевта? 5 вопросов
- Тест на тему Какие предметы сдавать для поступления на врача? 5 вопросов
- Тест на тему Какие экзамены нужно сдавать на учителя 5 вопросов
- Тест на тему Кадетский корпус - как поступить, чему учат и условия для проживания 5 вопросов
- Тест на тему Готовы ли вы к поступлению на психолога? 5 вопросов
- Тест на тему Готовы ли вы к поступлению на дизайнера? 5 вопросов
- Тест на тему Какие экзамены нужно сдавать на стюардессу? 5 вопросов
- Тест на тему Какие экзамены нужно сдавать на повара? 5 вопросов
- Тест на тему Какие предметы сдавать для поступления на программиста 5 вопросов
- Тест на тему Готовы ли вы сдавать экзамены на стоматолога? 5 вопросов
- Тест на тему Готовы ли вы сдавать экзамены на маркетолога? 5 вопросов
- Тест на тему Готовы ли вы сдавать экзамены на ветеринара? 5 вопросов
- Тест на тему Готовы ли вы поступать на экономиста? 5 вопросов
- Тест на тему Готовы ли вы к поступлению на юриста? 5 вопросов
- Тест на тему Готовы ли вы поступать на архитектора? 5 вопросов
- Тест на тему Характеристика Дуняши в романе “Тихий Дон” М. Шолохова 5 вопросов
- Тест на тему Описание образа Фамусова - персонажа комедии “Горе от ума” 5 вопросов
- Тест на тему Характеристика образа Сатина - персонажа пьесы “На дне” М. Горького 5 вопросов
- Тест на тему Анализ повести “Сашка” В. Кондратьева 5 вопросов
- Тест на тему Характеристика образа Фауста из трагедии Гёте 9 вопросов
- Тест на тему Анализ романа “Портрет Дориана Грея” О. Уайльда 5 вопросов
- Тест на тему Характеристика колобка - героя русской народной сказки 5 вопросов
- Тест на тему Образ главной героини “Алисы в стране чудес” Л. Кэррола 5 вопросов
- Тест на тему Трактовки образа Иисуса Христа в поэме “Двенадцать” А. Блока 5 вопросов
- Тест на тему Образ Настеньки из повести “Белые ночи” Ф. Достоевского 5 вопросов
- Тест на тему Конфликт в рассказе “После бала” Л. Толстого 5 вопросов
- Тест на тему Образ главной героини повести “Бедная Лиза” Н. Карамзина 5 вопросов
- Тест на тему Описание образа Васютки из рассказа “Васюткино озеро” В. Астафьева 5 вопросов
- Тест на тему Образы чиновников в комедии “Ревизор” Н. Гоголя 5 вопросов
- Тест на тему Роль образа вишневого сада в пьесе А. Чехова 5 вопросов
- Тест на тему Характеристика профессора Преображенского в повести “Собачье сердце” М. Булгакова 5 вопросов
- Тест на тему Описание образа городничего в комедии “Ревизор” Н. Гоголя 5 вопросов
- Тест на тему Описание образа главного героя “Доктора Живаго” Б. Пастернака 5 вопросов
- Тест на тему Образ Цыганка в повести “Детство” М. Горького 5 вопросов
- Тест на тему Характеристика Вани Солнцева в повести “Сын полка” В. Катаева 5 вопросов
- Тест на тему Образ автора в поэме "Василий Теркин" А. Твардовского 5 вопросов
- Тест на тему Образ портрета в повести "Портрет" Н. В. Гоголя 5 вопросов
- Тест на тему Описание образа девушки-ундины из “Героя нашего времени” М. Лермонтова 5 вопросов
- Тест на тему Описание образа Натальи Савишной в повести “Детство” Л. Толстого 5 вопросов
- Тест на тему Описание образа Костылина из “Кавказского пленника”. Л. Толстого 5 вопросов
- Тест на тему Описание образа Карла Ивановича в повести “Детство” Л. Толстого 5 вопросов
- Тест на тему Описание образа Жилина в “Кавказском пленнике” Л. Толстого 5 вопросов
- Тест на тему Описание образа Дины из “Кавказского пленника” Л. Толстого 5 вопросов
- Тест на тему Описание образа Вулича из “Героя нашего времени” М. Лермонтова 5 вопросов
- Тест на тему Описание образов татар в “Кавказском пленнике” Л. Толстого 5 вопросов
- Тест на тему Описание образа профессора Пирогова в рассказе “Чудесный доктор” А. Куприна 5 вопросов
- Тест на тему Народные образы героев в сказе «Серебряное копытце» П. Бажова 5 вопросов
- Тест на тему Описание образа Акакия Акакиевича Башмачкина из “Шинели” Н. Гоголя 5 вопросов
- Тест на тему Описание образов Лели и Миньки в одноименном рассказе М. Зощенко 5 вопросов
- Тест на тему Описание образа Сотникова из повести “Сотников” В. Быкова 5 вопросов
- Тест на тему Описание образов родителей в повести “Детство” Л. Толстого 5 вопросов
- Тест на тему Описание образа Флягина в “Очарованном страннике” Н. Лескова 5 вопросов
- Тест на тему Анализ комедии «Мещанин во дворянстве» Мольера 5 вопросов
- Тест на тему Описание образов героев рассказа “Галоша” М. Зощенко 5 вопросов
- Тест на тему Образ полковника - отца Вареньки из рассказа “После бала” Л. Толстого 5 вопросов
- Тест на тему Образ шинели в повести Н. В. Гоголя "Шинель" 5 вопросов
- Тест на тему Биография поэта Алексея Васильевича Кольцова 5 вопросов
- Тест на тему «Вечный зов» А. Иванова - краткое содержание 5 вопросов
- Тест на тему «Убийство в восточном экспрессе» А. Кристи - краткое содержание 5 вопросов
- Тест на тему Образ бабушки в повести «Детство» М. Горького 5 вопросов
- Тест на тему Описание образа барыни в рассказе «Муму» И. Тургенева 5 вопросов
- Тест на тему Главные произведения, написанные Александром Блоком 5 вопросов
- Тест на тему История создания песни “В лесу родилась елочка” 5 вопросов
- Тест на тему История создания поэмы “Двенадцать” А. Блока 5 вопросов
- Тест на тему История создания повести “Белые ночи” Ф. Достоевского 5 вопросов
- Тест на тему Аргументы к сочинению на тему: «Добро и зло в пьесе “Гроза” А. Островского» 5 вопросов
- Тест на тему Аргументы к сочинению 15.3 из пьесы «Горе от ума» 5 вопросов
- Тест на тему Аргументы к итоговому сочинению по рассказу «Матренин двор» А. Солженицына 5 вопросов
- Тест на тему Аргументы для итогового сочинения ЕГЭ по роману «Мастер и Маргарита» 5 вопросов
- Тест на тему Аргументы к итоговому сочинению по рассказу «Куст сирени» 5 вопросов
- Тест на тему Аргументы для итогового сочинения ЕГЭ по «Гарри Поттеру» 5 вопросов