Квадратные скобки в математике - значение, основные символы и примеры

Общая характеристика
Главная задача знаков — описание этапов осуществляемых действий. Математическое уравнение или выражение имеет одиночную пару квадратных, фигурных и других скобок, а также может использовать их некоторое количество.
Значение и разновидности
Скобки — это парные знаки, используемые во всевозможных областях. Чтобы правильно выстроить фразу в русском языке, для понимания смысла текста в предложении они употребляются как знаки препинания. С начальных классов школы изучают основы этих знаков.
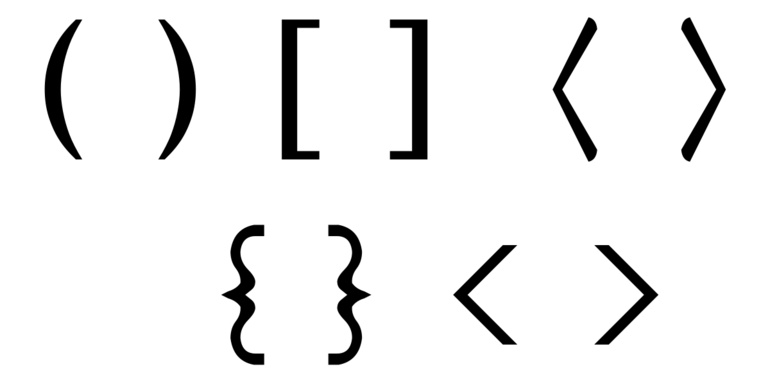
В расчетах первая из скобок считается открывающей, а вторая — замыкающей. Оба знака соответствуют друг другу, но также используются те, в которых открытие или закрытие не различается (косые /…/, прямые скобки |…|, двойные прямые ||…||. Раскрывать значение можно чаще всего в математике, физике, химии и остальных науках для указания важности выполнения операции в формулах. На компьютерной клавиатуре представлены все виды знаков препинания.
Разновидности:
- Круглые ().
- Квадратные [ ].
- Фигурные { }.
- Угловые ⟨ ⟩ (< > в ASCII-текстах).
Открытие круглых () произошло в 1556 году для подкоренного выражения. По правилу первым выполняется действие внутри знака, затем произведение или определение частного (деление), а в конце — суммирование и разница.
В Microsoft word, Excel включена электронная конфигурация этих знаков. Часто используемые виды скобок, следующие: (), [ ], { }(), [ ], { }. Также встречаются двойные, называемые обратными (]] и [ [) или << и >> в виде уголка. Их использование является двойственным — с открывающейся и замыкающей скобочкой.
Основные цели квадратной скобки в математике:
- Взятие целой части числового значения.
- Округление до близкого знака.
- Возведение в степень, взятие производной или подсчёт подинтегрального выражения.
- Приоритет операций. Примером может быть следующий способ: [(5+6)*2]3.
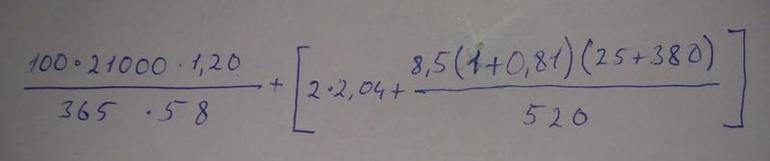
Другие варианты расчета:
- Векторное произведение — с = [a, b] = [a*b] = a*b.
- Закрытие сегмента [1;2] означает, что в множество включены цифры 1 и 2.
- Коммутатор [А, В = [А, В].
- Заменяют круглые скобки при записи матриц по правилам.
- Одна [ объединяет несколько уравнений или неравенств.
- Нотация Айверсона.
Квадратные скобки в математике обозначают, что действие выполняется последовательно. Эти знаки позволяют разграничить операции.
Треугольные актуальны в теории групп. Правило записи ⟨ a ⟩ n характеризует циклическую группу порядка n, сформированную элементом a.

Круглые (операторные) () используются в математике для описания первостепенности действий. Например, (1 +5)*3 означает, что нужно сначала сложить 1 и 5, а затем полученную величину перемножить на 3. Наряду с квадратными, используются для записи разных компонент векторов, матриц и коэффициентов.
На уроке математики преподаватель объясняет, как раскрыть скобки в уравнении для последующего решения. Фигурная одинарная { встречается при решении систем уравнений, обозначает пересечение данных, а [[ используется при их слиянии.
Одинарные или двойные выражения
Употребление [] происходит реже. Одно уравнение со скобками объединяет несколько значений или неравенств различных размеров. Для решения совокупности нужно выполнить любое условие. Конец, завершение действия замыкает закрывающий знак.
В персональных компьютерах, ноутбуках, нетбуках встроена кодировка Юникод, закрепленная не за левыми или правыми объединяющими знаками, а за открывающими и замыкающими, поэтому при воспроизведении печатного текста со скобочками в режиме «справа налево» каждый знак меняет внешнее направление на обратное.
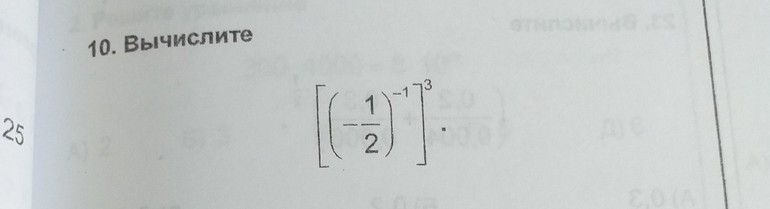
Квадратные скобки в уравнении означают, что установлен порядок действий, задаются границы промежутков и необходимость выполнения действия над выражением. Двойные квадратные скобки необходимы для записи выражений наряду с круглыми для рационального порядка действий.
По правилам интервал [−a;+a] записывается в виде нестрогого неравенства −a≤x≤a, означающего, что x находится на промежутке от −a до a включительно.
Также используются в математике как круглые, так и прямые знаки, означающие, что на конце отрезка, рядом с которым имеется круглая скобка, равенство строгое, а на том, где скобка квадратная — нестрогое. Интервал (−5;5] иначе записывается неравенством $5.
В середине парного знака с отделяющей точкой или запятой указываются два числа — наименьшее, затем большее, ограничивающие интервал. Круглая скобочка, прилегающая к цифре, означает невключение числа в промежуток, а квадратная — добавление.
В некоторых учебных пособиях для вузов встречаются расшифровки числовых интервалов, в которых вместо круглой скобочки (применяется обратная квадратная скобка ], и наоборот. В обозначениях запись ]0, 1[ равносильна (0, 1).
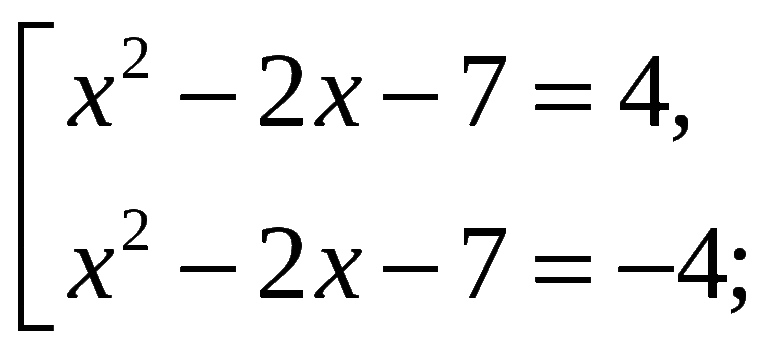
Открытая квадратная скобка (символ [) значит, что совокупность представляет систему уравнений разных размеров, для которых справедливы все множества решений для каждого уравнения, входящего в общее задание. Например, [x+11=2yy2−12=0
Прежде чем решать задачу или выполнять задание, нужно правильно определить принципы действий. В некоторых случаях скобочки могут быть не нужны, а иногда их обязательно нужно поставить.
Прочие знаки
Для математических, алгебраических и прочих расчетов важно знать различие обобщающих знаков. От правильности вычислений зависит итоговый результат.
Удобство записи системы уравнений
Система уравнений с объединяющими значками может раскрываться с помощью фигурной конфигурации{{. Это характеризует объединение неравенства или уравнений. Пример: {x2−1=0x2+x−2=0x2−1=0x2+x-2=0 или неравенства с несколькими переменными {x2−y>03x+2y≤3, cos x12 (x+π3)=02x2−4≥5x2-y>03x+2y≤3, cos x12x+π3=02x2−4≥5.
Применение фигурных знаков относится к представлению совмещения множеств. При решении системы с фигурной скобкой уравнения пересекаются, а [] объединяет их.

Кусочная функция изображается одиночной { скобкой, имеющей формулы, обусловливающие функцию, содержащие определенные промежутки. Пример:|x|={x, x≥0−x, x<0x=x, x≥0-x, x<0.
Для изображения координатных точек в виде промежутков, применяются круглые скобки. Они располагаются на координатной прямой, а также в прямоугольной системе или n-пространстве.
Запись двух координат А (1)А (2) означает, что т. АА имеет координату со значением 12, тогда Q (c, d, e) Q (c, d, e) свидетельствует о том, что т. QQ содержит координаты x, y, zx, y, z.
Множества задаются через перечисление элементов, входящих в эту область с помощью фигурных скобок, где участвующие элементы перечисляются через запятую. Пример: А={5, 6, 7, 8}А={5, 6, 7, 8}.
Для указания последовательности действий нужно заключить в скобочки выражения, уже содержащие скобки. Кроме обычных (круглых), используют знаки различной формы.
Примеры решений
Когда в скобки заключают выражение, содержащее круглые и квадратные скобки, пользуются фигурными знаками {}. Вычисление по таким формулам осуществляется в особом порядке: сначала считают внутри всех круглых скобок в определенной последовательности. Затем — внутри всех квадратных и фигурных.
Например, расчет предполагает поэтапное действие. Выражение последовательно 5 — 3 + 2 = 4. Если сначала сложить 3+2, затем отнять от 5−5 получится 0. Для указания правильной последовательности применяют скобки.
(5−2)+3 = 3+3 = 6.
7 — (2+2) = 7−4 = 3.
[(5+5) — (2−1)]+(6−4)= [(10 +1)] + 2= 11+2= 13.
Парные знаки не ставятся, если сложение и вычитание исполняются в указанной последовательности. Также когда внутри происходят операции умножения или деления.
По правилам сначала выполняются операции с цифрами в скобочках, а умножение или деление производятся в порядке их следования, ранее, чем сложение и вычитание. Исполняются остальные действия, а умножение и деление осуществляются в порядке их следования.
При использовании квадратных или фигурных знаков в начале вычисления начинаются внутри круглых скобочек, далее — внутри всех квадратных и фигурных. Оставшиеся действия происходят в последнюю очередь. Обобщающие знаки — скобки важны и незаменимы в математических расчетах для правильного вычисления.
Все тесты
- Биология
- История
- Сочинения
- Пунктуация
- Фонетический разбор
- Пушкин А.С
- Религия
- Карьера
- Информатика
- Физика
- Стихи
- Математика
- Обществознание
- ОБЖ
- Окружающий мир
- Экономика
- Биографии
- Анализ стихотворений
- Русский язык
- Краткие содержания
- Физкультура
- Орфография
- География
- Помощь студенту
- Литература
- Подготовка к ЕГЭ
- Тест на тему Что такое “железное легкое” и как жилось узникам аппарата 5 вопросов
- Тест на тему Суть и методы клеточной инженерии 5 вопросов
- Тест на тему Злаковые растения - общая характеристика, признаки и список представителей 7 вопросов
- Тест на тему Семейство бобовые - общая характеристика, строение и представители 7 вопросов
- Тест на тему Суть “дела Дрейфуса” и реакция общества 5 вопросов
- Тест на тему Деятельность партии монтаньяров во Франции 5 вопросов
- Тест на тему Традиции и обычаи украинского народа 5 вопросов
- Тест на тему Причины закрытия Японии в 17 веке и последствия 5 вопросов
- Тест на тему Подготовка и содержание генерального плана “Ост” 5 вопросов
- Тест на тему Тайны убийства Петра Столыпина 5 вопросов
- Тест на тему Отмена подушной подати на Руси 5 вопросов
- Тест на тему Период регентства Елены Глинской: события и реформы 5 вопросов
- Тест на тему Экономика России в годы Первой мировой войны 5 вопросов
- Тест на тему Битва при деревне Лесной 28 сентября 1708 года 5 вопросов
- Тест на тему 10 любопытных фактов про Рождество 5 вопросов
- Тест на тему 10 любопытных фактов про Новый год 5 вопросов
- Тест на тему История потешных полков Петра Первого 5 вопросов
- Тест на тему Образование и распад тушинского лагеря при Лжедмитрии II 5 вопросов
- Тест на тему Чем ведал и какие функции выполнял Разрядный приказ? 5 вопросов
- Тест на тему Задачи и направления внешней политики России в 16 веке 5 вопросов
- Тест на тему Установление и отмена бессрочного сыска беглых крестьян на Руси 5 вопросов
- Тест на тему История создания и деятельности Вольного экономического общества 5 вопросов
- Тест на тему Период правления Вещего Олега: внешняя и внутренняя политика 5 вопросов
- Тест на тему Правление и политика князя Игоря 5 вопросов
- Тест на тему Суть и последствия Нерчинского договора России с Китаем 1689 года 5 вопросов
- Тест на тему Причины, ход и итоги войны за польское наследство 1733-1735 гг. 5 вопросов
- Тест на тему Восстановление экономики СССР после Великой Отечественной Войны 5 вопросов
- Тест на тему Как и зачем были созданы полки иноземного строя 5 вопросов
- Тест на тему Создание стрелецких войск при Иване Грозном 5 вопросов
- Тест на тему Причины, ход событий и итоги выступления старообрядцев при Петре I 7 вопросов
- Тест на тему Как и почему началась Ливонская война: основные причины 5 вопросов
- Тест на тему К чему привела опричнина Ивана Грозного: последствия для страны 5 вопросов
- Тест на тему Положение черносошных крестьян на Руси 5 вопросов
- Тест на тему История Астраханского восстания: причины, события, итоги 7 вопросов
- Тест на тему Деятельность Великого посольства Петра I 5 вопросов
- Тест на тему Герои отечественной войны 1812 года - характеристика участников и полководцев 5 вопросов
- Тест на тему Развитие системы образования и науки в первой половине 19 века 6 вопросов
- Тест на тему Первые князья Киевской Руси - даты правления и особенности проводимой политики 7 вопросов
- Тест на тему Характеристика, периоды развития жизни в Палеозойскй эре 7 вопросов
- Тест на тему История праздника 23 февраля - происхождение и значение для России 7 вопросов
- Тест на тему Кто придумал отмечать 8 марта: история праздника 8 вопросов
- Тест на тему Славянские праздники - список праздников, обрядов и обычаев славян 10 вопросов
- Тест на тему Образ Шарикова в повести «Собачье сердце» М. Булгакова 5 вопросов
- Тест на тему Образы героев в повести «Невский проспект» Н. Гоголя 5 вопросов
- Тест на тему Московские главы в романе «Мастер и Маргарита» Булгакова 7 вопросов
- Тест на тему Описание образа бирюка из рассказа И. Тургенева 7 вопросов
- Тест на тему Образы героев в романе «Отцы и дети» И. Тургенева 7 вопросов
- Тест на тему Образы героев в повести «Котлован» А. Платонова 7 вопросов
- Тест на тему Образы героев в пьесе «Гроза» А. Островского 7 вопросов
- Тест на тему История создания повести Н. В. Гоголя “Шинель” 7 вопросов
- Тест на тему История создания сборника рассказов Тургенева “Записки охотника” 7 вопросов
- Тест на тему История создания повести "Муму" Ивана Тургенева 7 вопросов
- Тест на тему История создания стихотворения "Реквием" Анны Ахматовой 10 вопросов
- Тест на тему История создания повести Гоголя "Тарас Бульба" 10 вопросов
- Тест на тему История создания стихотворения Пушкина "Деревня" 6 вопросов
- Тест на тему История создания стихотворения М. Лермонтова “Нищий” 7 вопросов
- Тест на тему История создания стихотворения "Она сидела на полу" 7 вопросов
- Тест на тему История создания Пушкиным стихотворения "К морю" 6 вопросов
- Тест на тему История создания повести «Станционный смотритель» А. Пушкина 10 вопросов
- Тест на тему История создания «Оды на день восшествия» М. Ломоносова 7 вопросов
- Тест на тему "Банты" - как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Конечно же» - выделяется ли слово запятыми? 5 вопросов
- Тест на тему «Подчеркивать» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Лифты» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Строку» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Апостроф» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Зубчатый» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Прозорлива» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Балашиха» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Реку» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Полно» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Говорено» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Досыта» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Упрочение» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Развила» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Подолгу» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Логин» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Окон» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Втридорога» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Утра» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Запломбированный» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Цыган» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Шарфы» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Бармен» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Положенный» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Крадущийся» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Донизу» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Явишься» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Ободрить» - как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Предприняв» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Прочтено» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Низок» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Исчерпать» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Роба» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Исчерпывающий» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Будучи» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Понятым» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Повторен» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Изредка» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Донельзя» − как ставить ударение в слове? 5 вопросов
- Тест на тему «Загодя» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Принужден» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Опошлить» − как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Краны» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Торты» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Инструмент» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Брало» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Забрала» − как правильно ставить ударение? 5 вопросов
- Тест на тему «Отзыв» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Рефлексия» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему Как люди узнают о том, что было в прошлом? 5 вопросов
- Тест на тему Какие животные впадают в спячку зимой: объяснения зоологов 7 вопросов
- Тест на тему Сообщение по окружающему миру для 4 класса об острове Врангеля 5 вопросов
- Тест на тему Сообщение о морских обитателях - описание, виды и названия 7 вопросов
- Тест на тему Биография поэта и писателя Льва Рубинштейна 5 вопросов
- Тест на тему Биография президента Белоруссии Александра Лукашенко 5 вопросов
- Тест на тему 10 интересных фактов про Афанасия Фета 5 вопросов
- Тест на тему 10 интересных фактов про Ивана Тургенева 5 вопросов
- Тест на тему Биография писателя и поэта Вячеслава Урюпина 5 вопросов
- Тест на тему Биография поэта Николая Михайловича Рубцова 5 вопросов
- Тест на тему Биография поэта Андрея Дмитриевича Дементьева 5 вопросов
- Тест на тему Биография президента РФ Владимира Путина 5 вопросов
- Тест на тему Биография и личная жизнь Даниила Хармса 5 вопросов
- Тест на тему Краткая биография Валентины Осеевой 5 вопросов
- Тест на тему Григорий Остер: биография писателя и избранные произведения 7 вопросов
- Тест на тему Елена Благинина: творческая биография и личная жизнь 10 вопросов
- Тест на тему Биография детской писательницы Ирины Пивоваровой 5 вопросов
- Тест на тему Анализ стихотворения «Догорел апрельский светлый вечер…» И. Бунина 5 вопросов
- Тест на тему Анализ стихотворения «Фонтан» Ф. Тютчева 5 вопросов
- Тест на тему Анализ стихотворения «Посмотри - какая мгла» Я. Полонского 5 вопросов
- Тест на тему Анализ стихотворения «Школьник» Н. Некрасова 5 вопросов
- Тест на тему Анализ стихотворения «Несжатая полоса» Н. Некрасова 5 вопросов
- Тест на тему «Весенний дождь» - анализ стихотворения А.А. Фета 7 вопросов
- Тест на тему «Поет зима - аукает» - анализ стихотворения С.А. Есенина 7 вопросов
- Тест на тему Сообщение на тему: «Традиции русской речевой манеры общения» 5 вопросов
- Тест на тему Определение и виды простых осложненных предложений 5 вопросов
- Тест на тему Какие бывают виды текстов? 5 вопросов
- Тест на тему Образование и правописание страдательных причастий настоящего времени 5 вопросов
- Тест на тему Как определить начальную форму прилагательного? 5 вопросов
- Тест на тему Местоимение-прилагательное в русском языке 5 вопросов
- Тест на тему Сборник правил по русскому языку для 6 класса 7 вопросов
- Тест на тему Сборник правил по русскому языку за 5 класс 7 вопросов
- Тест на тему Упражнения для тренировки школьников 7 класса по причастному обороту 9 вопросов
- Тест на тему Тест: Склонение фамилий в русском языке 7 вопросов
- Тест на тему Общеупотребительные и необщеупотребительные слова 5 вопросов
- Тест на тему Дефисное и слитное написание сложных прилагательных 5 вопросов
- Тест на тему Морфологический разбор числительного - правило и примеры 5 вопросов
- Тест на тему «Акула» Л. Толстого - краткое содержание 5 вопросов
- Тест на тему Русская народная сказка «Хвосты» - краткое содержание 5 вопросов
- Тест на тему Краткое содержание оперы «Снегурочка» Римского-Корсакова 5 вопросов
- Тест на тему «Обезьяний язык» М. Зощенко – краткое содержание 10 вопросов
- Тест на тему «Сердце не камень» - краткое содержание пьесы А.Н. Островского 5 вопросов
- Тест на тему Балет «Щелкунчик» — краткое содержание 7 вопросов
- Тест на тему Реферат по физкультуре на тему: «Здоровое питание» 5 вопросов
- Тест на тему История развития лыжного спорта в разных странах - классификация и интересные факты 6 вопросов
- Тест на тему Важность самоконтроля при занятиях спортом 5 вопросов
- Тест на тему Как выполняются прыжки через козла? 5 вопросов
- Тест на тему Что такое здоровый образ жизни? 5 вопросов
- Тест на тему Как правильно выполнять кувырки? 5 вопросов
- Тест на тему Развитие гибкости тела: упражнения и польза для тела 5 вопросов
- Тест на тему Виды и польза прыжков через скакалку 5 вопросов
- Тест на тему Какие есть зимние виды спорта? 5 вопросов
- Тест на тему Реферат на тему: “Гимнастика как вид спорта” 8 вопросов
- Тест на тему Реферат по физкультуре на тему “Футбол” 7 вопросов
- Тест на тему Реферат по физкультуре на тему: “Баскетбол - виды и лиги” 7 вопросов
- Тест на тему Реферат на тему «Лыжный спорт» 10 вопросов
- Тест на тему Реферат по физической культуре «Формы и виды закаливания» 10 вопросов
- Тест на тему Правописание слов с непроверяемой безударной гласной в корне 5 вопросов
- Тест на тему Нужно ли ставить запятую к фразе - "с уважением"? 5 вопросов
- Тест на тему «Во-вторых» или «во вторых» – как правильно пишется? 5 вопросов
- Тест на тему "Нету" или "нет" - как правильно писать и говорить? 5 вопросов
- Тест на тему «Не я» или «нея» – как правильно пишется? 5 вопросов
- Тест на тему «Полным-полно» или «полным полно» - как правильно пишется? 5 вопросов
- Тест на тему Как пишется «кто-нибудь» или «кто нибудь»? 5 вопросов
- Тест на тему Мягкий знак после шипящих в глаголах - правила, примеры 5 вопросов
- Тест на тему «Потвёрже» или «по твёрже» – как правильно пишется? 5 вопросов
- Тест на тему «Какой-то» или «какой то» – как пишется правильно? 5 вопросов
- Тест на тему «Мало-помалу» или «мало помалу» – как правильно пишется? 5 вопросов
- Тест на тему «По-осеннему» или «по осеннему» – как правильно пишется? 5 вопросов
- Тест на тему "Находу" или "на ходу" - слитно или раздельно писать? 5 вопросов
- Тест на тему "ЮлИчка" или "ЮлЕчка" - как правильно писать? 5 вопросов
- Тест на тему «Не пойму» или «непойму» – как правильно пишется? 5 вопросов
- Тест на тему «Доброе утро» − как правильно пишется? 5 вопросов
- Тест на тему «Почему-то» или «почему то» – как правильно пишется? 5 вопросов
- Тест на тему «На вынос» или «навынос» – как правильно пишется? 5 вопросов
- Тест на тему «Невежливо» или «не вежливо» – как правильно пишется? 5 вопросов
- Тест на тему «Негодуя» или «не годуя» - как правильно пишется? 5 вопросов
- Тест на тему «КуриНый» или «куриННый» − как правильно пишется? 5 вопросов
- Тест на тему «ТеННис» или «теНис» – как правильно пишется? 5 вопросов
- Тест на тему «ТумаННый» или «тумаНый» – как правильно пишется? 5 вопросов
- Тест на тему «ЗамечеННый» или «замечеНый» – как правильно пишется? 5 вопросов
- Тест на тему «Семнадцать» или «семЬнадцать» – как правильно пишется? 5 вопросов
- Тест на тему «ВыздОравливающий» или «выздАравливающий» – как правильно пишется? 5 вопросов
- Тест на тему «Свеж» или «свежЬ» – как правильно пишется? 5 вопросов
- Тест на тему «СлаЩе» или «слаДЧе» – как правильно пишется? 5 вопросов
- Тест на тему «ПрЕтерпевать» или «прИтерпевать» - как правильно пишется? 5 вопросов
- Тест на тему «Удастся» или «удастЬся» – как правильно пишется? 5 вопросов
- Тест на тему «СписаНо» или «СписаННо» – как правильно пишется? 5 вопросов
- Тест на тему «Происшествие» или «проишествие» – как правильно пишется? 5 вопросов
- Тест на тему «НачИнающий» или «начЕнающий» – как правильно пишется? 5 вопросов
- Тест на тему «Невозможно» или «не возможно» – как пишется слитно или раздельно? 5 вопросов
- Тест на тему «Налету» или «на лету» – как правильно пишется? 5 вопросов
- Тест на тему «Надолго» или «на долго» – как правильно пишется? 5 вопросов
- Тест на тему «ПьющАя» или «пьющЕя» – как правильно пишется? 5 вопросов
- Тест на тему «Неужели» или «не ужели» − как правильно пишется? 5 вопросов
- Тест на тему «НИкого» или «нЕкого» – как правильно пишется? 5 вопросов
- Тест на тему «БаССейн» или «баСейн» − как правильно пишется? 5 вопросов
- Тест на тему "Не согласованно" или "несогласованно" - слитно или раздельно? 5 вопросов
- Тест на тему «ОбстОятельствам» или «обстАятельствам» – как правильно пишется? 5 вопросов
- Тест на тему «ОбижеННый» или «обижеНый» – как правильно пишется? 5 вопросов
- Тест на тему «Аллах» или «Алах» – как правильно пишется? 5 вопросов
- Тест на тему «БелОрусский» или «белАрусский» – как правильно пишется? 5 вопросов
- Тест на тему «ЧИсло» или «чЕсло» – как правильно пишется? 5 вопросов
- Тест на тему «УвЕряющий» или «увИряющий» – как правильно пишется? 5 вопросов
- Тест на тему «НенасТный» или «ненасный» – как правильно пишется? 5 вопросов
- Тест на тему «Постричь» или «поДстричь» – как правильно пишется? 5 вопросов
- Тест на тему «КоЛея» или «коЛЛея» – как правильно пишется? 5 вопросов
- Тест на тему Характеристика природных зон Поволжья 5 вопросов
- Тест на тему Для каких рек в России характерно летнее половодье? 5 вопросов
- Тест на тему Как правильно заполнять дневник наблюдения за погодой 5 вопросов
- Тест на тему Влажные экваториальные леса - особенности климата, характеристика флоры и фауны 7 вопросов
- Тест на тему Европейский север России - географическое положение, особенности развития предприятий и промышленности 7 вопросов
- Тест на тему Что такое масштаб карты и как его определять 7 вопросов
- Тест на тему Особенности и примеры островных государств 5 вопросов
- Тест на тему Природные зоны Южной Америки - характеристики и особенности 7 вопросов
- Тест на тему 10 интересных фактов про океан 7 вопросов
- Тест на тему Сектор Газа: где он находится и откуда такое название? 6 вопросов
- Тест на тему Что нужно сдавать на бухгалтера? 5 вопросов
- Тест на тему Какие предметы нужно сдавать на пилота 5 вопросов
- Тест на тему Какие экзамены нужно сдавать на фотографа? 5 вопросов
- Тест на тему Какие предметы нужно сдавать на хореографа? 5 вопросов
- Тест на тему Какие предметы нужно сдавать на актера? 5 вопросов
- Тест на тему Какие предметы нужно сдавать на режиссера? 5 вопросов
- Тест на тему Что нужно сдавать на художника? 5 вопросов
- Тест на тему Что нужно сдавать для поступления на визажиста? 5 вопросов
- Тест на тему Какие экзамены нужно сдавать на полицейского? 5 вопросов
- Тест на тему Какие предметы нужно сдавать на фармацевта? 5 вопросов
- Тест на тему Какие предметы сдавать для поступления на врача? 5 вопросов
- Тест на тему Какие экзамены нужно сдавать на учителя 5 вопросов
- Тест на тему Кадетский корпус - как поступить, чему учат и условия для проживания 5 вопросов
- Тест на тему Готовы ли вы к поступлению на психолога? 5 вопросов
- Тест на тему Готовы ли вы к поступлению на дизайнера? 5 вопросов
- Тест на тему Какие экзамены нужно сдавать на стюардессу? 5 вопросов
- Тест на тему Какие экзамены нужно сдавать на повара? 5 вопросов
- Тест на тему Какие предметы сдавать для поступления на программиста 5 вопросов
- Тест на тему Готовы ли вы сдавать экзамены на стоматолога? 5 вопросов
- Тест на тему Готовы ли вы сдавать экзамены на маркетолога? 5 вопросов
- Тест на тему Готовы ли вы сдавать экзамены на ветеринара? 5 вопросов
- Тест на тему Готовы ли вы поступать на экономиста? 5 вопросов
- Тест на тему Готовы ли вы к поступлению на юриста? 5 вопросов
- Тест на тему Готовы ли вы поступать на архитектора? 5 вопросов
- Тест на тему Характеристика Дуняши в романе “Тихий Дон” М. Шолохова 5 вопросов
- Тест на тему Описание образа Фамусова - персонажа комедии “Горе от ума” 5 вопросов
- Тест на тему Характеристика образа Сатина - персонажа пьесы “На дне” М. Горького 5 вопросов
- Тест на тему Анализ повести “Сашка” В. Кондратьева 5 вопросов
- Тест на тему Характеристика образа Фауста из трагедии Гёте 9 вопросов
- Тест на тему Анализ романа “Портрет Дориана Грея” О. Уайльда 5 вопросов
- Тест на тему Характеристика колобка - героя русской народной сказки 5 вопросов
- Тест на тему Образ главной героини “Алисы в стране чудес” Л. Кэррола 5 вопросов
- Тест на тему Трактовки образа Иисуса Христа в поэме “Двенадцать” А. Блока 5 вопросов
- Тест на тему Образ Настеньки из повести “Белые ночи” Ф. Достоевского 5 вопросов
- Тест на тему Конфликт в рассказе “После бала” Л. Толстого 5 вопросов
- Тест на тему Образ главной героини повести “Бедная Лиза” Н. Карамзина 5 вопросов
- Тест на тему Описание образа Васютки из рассказа “Васюткино озеро” В. Астафьева 5 вопросов
- Тест на тему Образы чиновников в комедии “Ревизор” Н. Гоголя 5 вопросов
- Тест на тему Роль образа вишневого сада в пьесе А. Чехова 5 вопросов
- Тест на тему Характеристика профессора Преображенского в повести “Собачье сердце” М. Булгакова 5 вопросов
- Тест на тему Описание образа городничего в комедии “Ревизор” Н. Гоголя 5 вопросов
- Тест на тему Описание образа главного героя “Доктора Живаго” Б. Пастернака 5 вопросов
- Тест на тему Образ Цыганка в повести “Детство” М. Горького 5 вопросов
- Тест на тему Характеристика Вани Солнцева в повести “Сын полка” В. Катаева 5 вопросов
- Тест на тему Образ автора в поэме "Василий Теркин" А. Твардовского 5 вопросов
- Тест на тему Образ портрета в повести "Портрет" Н. В. Гоголя 5 вопросов
- Тест на тему Описание образа девушки-ундины из “Героя нашего времени” М. Лермонтова 5 вопросов
- Тест на тему Описание образа Натальи Савишной в повести “Детство” Л. Толстого 5 вопросов
- Тест на тему Описание образа Костылина из “Кавказского пленника”. Л. Толстого 5 вопросов
- Тест на тему Описание образа Карла Ивановича в повести “Детство” Л. Толстого 5 вопросов
- Тест на тему Описание образа Жилина в “Кавказском пленнике” Л. Толстого 5 вопросов
- Тест на тему Описание образа Дины из “Кавказского пленника” Л. Толстого 5 вопросов
- Тест на тему Описание образа Вулича из “Героя нашего времени” М. Лермонтова 5 вопросов
- Тест на тему Описание образов татар в “Кавказском пленнике” Л. Толстого 5 вопросов
- Тест на тему Описание образа профессора Пирогова в рассказе “Чудесный доктор” А. Куприна 5 вопросов
- Тест на тему Народные образы героев в сказе «Серебряное копытце» П. Бажова 5 вопросов
- Тест на тему Описание образа Акакия Акакиевича Башмачкина из “Шинели” Н. Гоголя 5 вопросов
- Тест на тему Описание образов Лели и Миньки в одноименном рассказе М. Зощенко 5 вопросов
- Тест на тему Описание образа Сотникова из повести “Сотников” В. Быкова 5 вопросов
- Тест на тему Описание образов родителей в повести “Детство” Л. Толстого 5 вопросов
- Тест на тему Описание образа Флягина в “Очарованном страннике” Н. Лескова 5 вопросов
- Тест на тему Анализ комедии «Мещанин во дворянстве» Мольера 5 вопросов
- Тест на тему Описание образов героев рассказа “Галоша” М. Зощенко 5 вопросов
- Тест на тему Образ полковника - отца Вареньки из рассказа “После бала” Л. Толстого 5 вопросов
- Тест на тему Образ шинели в повести Н. В. Гоголя "Шинель" 5 вопросов
- Тест на тему Биография поэта Алексея Васильевича Кольцова 5 вопросов
- Тест на тему «Вечный зов» А. Иванова - краткое содержание 5 вопросов
- Тест на тему «Убийство в восточном экспрессе» А. Кристи - краткое содержание 5 вопросов
- Тест на тему Образ бабушки в повести «Детство» М. Горького 5 вопросов
- Тест на тему Описание образа барыни в рассказе «Муму» И. Тургенева 5 вопросов
- Тест на тему Главные произведения, написанные Александром Блоком 5 вопросов
- Тест на тему История создания песни “В лесу родилась елочка” 5 вопросов
- Тест на тему История создания поэмы “Двенадцать” А. Блока 5 вопросов
- Тест на тему История создания повести “Белые ночи” Ф. Достоевского 5 вопросов
- Тест на тему Аргументы к сочинению на тему: «Добро и зло в пьесе “Гроза” А. Островского» 5 вопросов
- Тест на тему Аргументы к сочинению 15.3 из пьесы «Горе от ума» 5 вопросов
- Тест на тему Аргументы к итоговому сочинению по рассказу «Матренин двор» А. Солженицына 5 вопросов
- Тест на тему Аргументы для итогового сочинения ЕГЭ по роману «Мастер и Маргарита» 5 вопросов
- Тест на тему Аргументы к итоговому сочинению по рассказу «Куст сирени» 5 вопросов
- Тест на тему Аргументы для итогового сочинения ЕГЭ по «Гарри Поттеру» 5 вопросов







