Понятие и основные определения

Впервые с понятием линейное неравенство школьники сталкиваются на уроках алгебры в восьмом классе. Неравенства линейного вида тесно связаны с функциями, графиком которых является прямая линия. Применительно это к выражениям, в которых существует одна вещественная переменная. Для функции c одной переменной справедлива запись: f = dx + b. Если последний член равенства равен нулю, то такую функцию называют однородной, в ином же случае — неоднородной.

В математике принято под неравенством понимать отношение, при котором можно использовать один из следующих двух знаков:

• q < b — меньше, обозначает, что левое выражение численно меньше правого;
• q > b — больше, показывает, что значение левого выражения больше правого.

Вместе с двумя основными знаками может использоваться и равенство. Таким образом, в математике неравенства разделяют на строгие (без знака равно) и нестрогие.

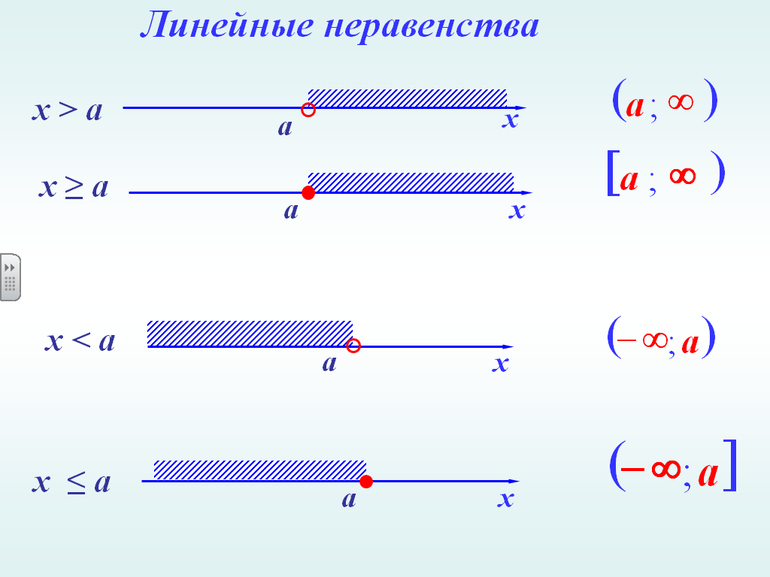
Если одна и та же переменная входит в различные выражения, то их можно связать между собой в систему. Для линейного неравенства с одной переменной присущ одна особенность. Неизвестная в нём не может стоять в степени отличной от единицы или на неё делиться другое число. Иными словами, график выражений со второй, кубической, квадратической и другой степенью будет иметь вид отличный от прямой.

Совокупность таких уравнений является равносильной. Поэтому при решении часто используется подход замены сложных выражений простыми. Известными членами в уравнении могут быть рациональные, иррациональные и логарифмические числа. Для записи ответа используется как цифровое, так и графическое обозначение.

На рисунке уравнение представляется как полуплоскость. В случае строгого неравенства непосредственно прямая не входит в ответ. Для определения, какая же полуплоскость соответствует множеству решений, определяют значение в произвольной точке и проверяют, удовлетворяет ли число знаку неравенства.

Принцип решения

Алгоритм решения линейных неравенств базируется на их свойствах и нескольких правилах. Под решением неравенства понимают нахождение множества значений переменных, подстановка которых в уравнение превращает его в верное числовое выражение.

При нахождении неизвестных в уравнении используют пять свойств числовых неравенств:

1. Когда первый член больше второго, а его значение превышает величину третьего, то отсюда следует, что первый будет больше третьего. Например, 12 > 11 и 11 > 5, то 12 > 5.

2. Если значение первой части неравенства больше чем второго, то при изменении на одинаковое число обеих частей, знак неравенства останется неизменным. Например, 2 k + 3 > 0, соответствует: 2 k + 3 + 19 > 0 + 19.
3. Когда первая часть превышает значение второй и при этом существует число больше нуля, то при умножении обеих частей на это значение знак неравенства не изменится. Например, 9 > 4, а 2 > 0, то записать 9*2 > 4*2 будет также верной.
4. Если существует зависимость вида f > n и p > k, то f + p > n + k. Например, если 11 > 6 и 5 > 3, то 11 + 5 > 6 + 3.
5. При положительных значениях членов уравнения и выполнении условия, при котором первый элемент больше второго, а третий четвёртого, верным будет считаться, что произведение первого с третьим членом будет больше второго с четвёртым. Например, если 11 > 5 и 4 > 3, то 11*4 > 5*3.

Исходя из указанных свойств делают выводы, что слагаемое можно переносить из одной части уравнения в другую изменив при этом знак на противоположный. При умножении или делении обеих частей выражения на одно и то же значение знак неравенства не изменяется. Это утверждение также справедливо к другим арифметическим действиям с любым видом чисел. Следует заметить, что если обе стороны умножаются на число с отрицательным знаком, то знак неравенства меняется на противоположный.

Касательно систем действует правило, заключающееся в том, что если в совокупности нет уравнений, которые можно сократить, то в этом случае удалить уравнения без изменения решений не выйдет. Так как решить неравенство означает найти все значения переменных, при которых оно будет верным, то множество всех таких решений состоит из эквивалентных корней.

Для решения же линейного уравнения с двумя переменными необходимо найти пару значений неизвестных по оси абсцисс и ординат, обращающую его в верное числовое выражение. Поэтому ответ в таких выражениях изображают в виде графика с указанием области искомого множества. При этом решение системы с двумя и более переменными находят по области пересечения каждого уравнения.

Простой пример

Решение линейных неравенств построено на чётком порядке действий. Самый простой способ — это использование метода тождественных преобразований. По сути, это сведение задания непосредственно к ответу. Например, пусть дано неравенство: p + 3 > 5*p — 5. Для его решения нужно выполнить следующую последовательность шагов:

1. Члены с неизвестными переменными перенести в одну сторону, а свободные — в другую. Сложность здесь заключается в правильном изменении знаков. Нужно помнить, что у переносимых членов знак меняется на противоположный: p — 5*p > -5 — 3.
2. Так как члены в правой и левой части теперь однотипные, то с ними можно выполнить арифметические действия. В итоге получится выражение: -4*p > - 8.
3. Используя правило, разрешающее выполнять с обеими сторонами однотипные и равные действия для упрощения выражения, следует каждый член разделить на -4. Тогда знак изменится на противоположный: p < 2.

Полученное выражение и является искомым ответом. Обозначают его как p Є (-ɷ, 2). Тут важно обратить внимание на то, что в записи используются круглые скобки. Для наглядности ответ можно нарисовать на числовой оси. Конечно же, для простых примеров графически изображать ответ не имеет особого смысла, так как и всё довольно просто, но вот для систем или неравенств с двумя переменными график просто необходим.

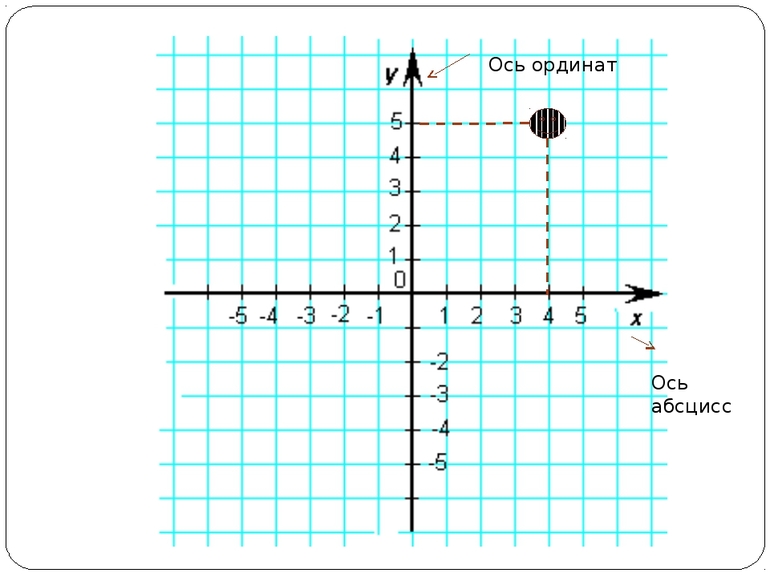
Для рассматриваемого примера следует нарисовать ось p с отложенной на ней цифрой два. На рисунке число обозначается незакрашенной точкой. Это указывает на то, что сама двойка в ответ не входит. Полученный ответ строгий, так что все числа, располагающиеся с левой стороны от двойки, входят в искомое множество решений, то есть удовлетворяют условию задания.

Если неравенство не строгое, то есть содержит знак равенства, то точка изображается закрашенной, а в ответе используется квадратная скобка. Например, условие задачи p ≥ - 10, обозначается как p Є [ -10; + ɷ). Бесконечность не может быть записана в квадратной скобке, так как это не число. Форму, использующую разные скобки, удобно применять для записи сложных ответов.

Тригонометрические уравнения

Показательным тригонометрическим линейным уравнением является выражение: cosx > c, где c любое действительное число. Чтобы решить это задание строят числовую окружность. На оси х находят точку, соответствующую значению числа. На окружности с помощью параллельной линии оси абсцисс отмечают две точки, в которых происходит пересечение.

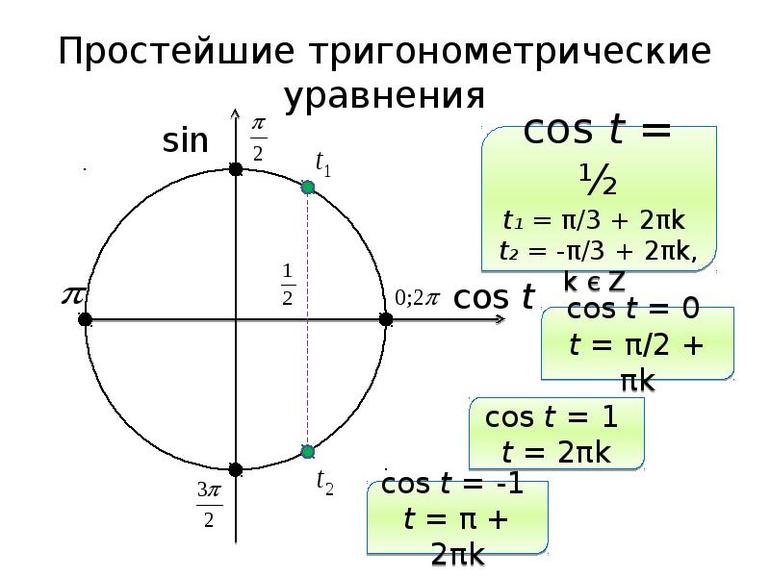
Используя правила обратных тригонометрических функций можно утверждать, что верхняя точка соответствует arccos c, а симметричная ей -arccos c. Так как по условию задачи cosx > c, то неравенство будет соответствовать значениям, располагающимся в правой части от проведённой линии. Соответственно, верным решением будет любая точка, располагающаяся на дуге между arccos c и -arccos c. Поэтому можно записать: c Є (- arccosc + 2pk, arccosc + 2pk).

Например, необходимо решить дробное неравенство: cos c ≤ (2)^½/2. Для нахождения решений на графике отмечают точку, соответствующую корню из двух пополам, и проводят вертикальную линию. Одна точка пересечения будет равна р/4, а другая -р/4. Так как косинус меньше, то возможные решения располагаются в левой части, то есть от р/4 до -р/4. Чтобы ответ записать от меньшего к большему, к -р/4 добавляют 2р. Тогда решением линейного неравенства с одной переменной будет: c Є [р/4 + 2pk, 7р/4 + 2pk].

По аналогии решаются задания с синусом, котангенсом и тангенсом. При нахождении ответа подробный анализ выполнять необязательно. Необходимо просто использовать простейшие тригонометрические формулы. Так для sin c > 1/ 2, будет верным решение с Є (p /6 + 2 p k, 5 p /6 + 2 pk), а для строгой записи tg ≥ с: c Є ≥ [p /4 + p k, p /2 + p k]. В ответ добавляется рк, так как помимо верхнего промежутка на графике есть симметричный ему другой интервал, повторяющийся через p.

Система с неизвестными

Уравнения с одной и той же переменной, при сравнении с разным свободным членом, называют при объединении системой линейных неравенств. Для решения такого рода примеров необходимо найти ответ для каждого неравенства отдельно, а затем указать все переменные, удовлетворяющие каждому выражению. Система может содержать бесконечное множество уравнений.

Например, необходимо вычислить множество решений следующего неравенства:

{2c — 4 ≥ 0,

{5c -15 > 0.

Выполняя простейшие преобразования, рассматриваемую систему можно привести к виду:

{2c ≥ 4,

{5c > 15.

Ответом для первого уравнения будет с ≥ 2, а второго с > 3. Решением системы будут такие значения, которые удовлетворяют обоим уравнениям. Очень часто используют чертёж. На нём изображают две числовые прямые друг под другом. На одной отмечают число два, а на втором три. Области, которые соответствуют решению, закрашивают. После этого визуально становится понятным, какая часть будет являться общим решением. В рассматриваемом примере c > 3. То есть c принадлежит от трёх до плюс бесконечности.

Неравенства с двойной переменной — это выражения вида f (x, y) > 0, при этом знак в выражении может быть любым. Решать примеры такого вида удобно, используя графический метод. Например, пусть x* y < 1. Следует рассмотреть три случая:

1. х = 0. При подстановке в выражение нуля неравенство будет верным, поэтому х = 0 и является решением.
2. х > 0. В этом случае это выражение можно разделить на х и выражение будет иметь вид y < 1/x.
3. х < 0. При этом предположении можно записать: y > 1/x.

Изобразив все эти решения, на координатной плоскости получают две гиперболы, пространство между которыми будет являться ответом рассматриваемого неравенства.

Например, модуль x плюс модуль y меньше либо равно двум. Для решения нужно рассмотреть всевозможные значения модуля: x ≥ 0, y ≥ 0. Отложить точки на осях координат и соединить их, получится прямоугольник, в середине которого будет находиться искомое множество решений.

Применение онлайн-калькуляторов

Во всемирной сети существуют сервисы, позволяющие вычислять линейные уравнения буквально в течение нескольких секунд. С их помощью решить неравенство любой сложности сможет даже пользователь, совершенно не понимающий методы, используемые для нахождения ответов.

Эти порталы привлекательны ещё и тем, что каждый выполненный шаг при решении подробно описывается. Появление ошибки при расчёте невозможно. Поэтому эти сайты востребованы даже у математиков, рассчитывающих целые и дробные выражения.

Чтобы получить ответ, регистрироваться не нужно. Необходимо просто зайти на сайт с помощью веб-обозревателя и указать заданное неравенство. Как только искомое выражение будет вписано, следует кликнуть по меню «Рассчитать» и получить ответ с пошаговым решением.