Доверительный интервал - формула и примеры определения вероятности

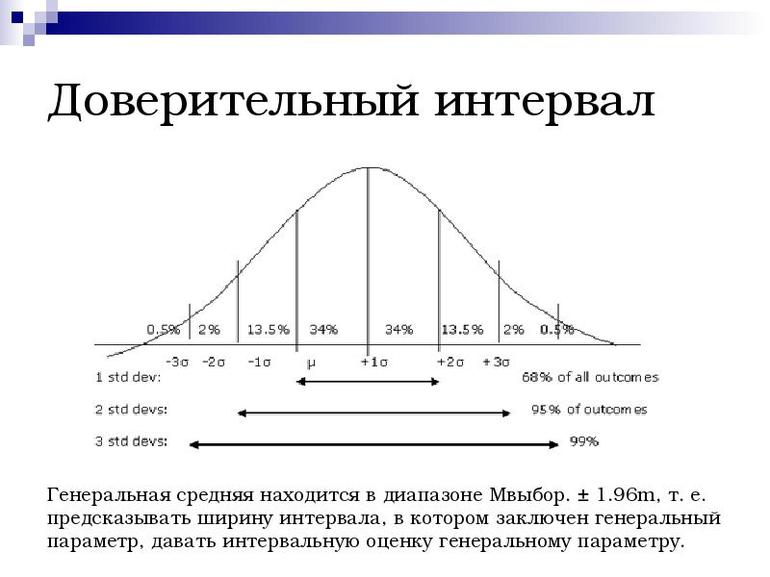
Общая схема построения

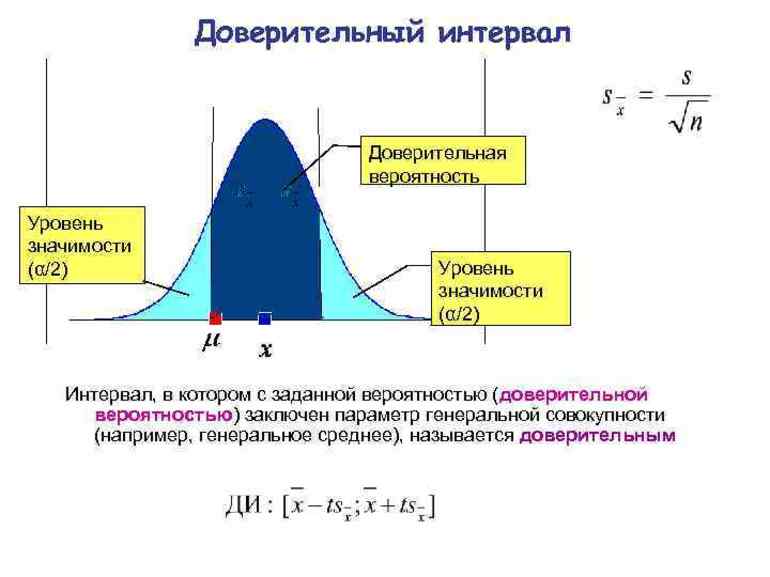
По сути, метод основан на модели классической математической статистики, подразумевающей бесконечно возможные выборки в генеральной совокупности. Пусть имеется главная выборка эпсилон с функцией распределения известной до некого параметра тау (Fe (x, τ)). Из этой генеральной совокупности получена выборка объёмом эн, включающая диапазон от x1 до xn. Этот параметр можно считать одномерным и принадлежащим диапазону от τ до R. Математически такое положение описывают как τ є T c R.

Если предположить, что для некоторого интервала йод, лежащего от нуля до единицы, существуют статистики S-(X|n|, J) и S+(X|n|, J), при этом им соответствует неравенство P{ S-(X|n|, J) < τ < S+(X|n|, J)}, то рассматриваемый интервал принято называть доверительным касательно параметра τ. Причём уровень доверия или величина доверительного интервала зависит от значения статистики S и выборки. Вероятность попадания истинного параметра тэта в интервал от S-1 до S+1 находится из выражения: P = 1 — J.

Общий метод построения доверительных функций может быть использован при изучении статистики Y (S (X|n|, t), где: t — оцениваемый параметр, S (X|n| - точечная оценка. При этом известны следующие свойства:

• функция распределения Fy (x), где игрек принимает случайное известное значение, не подвержена влиянию тау.
• график функция статистики непрерывный и монотонный по тау.

После того как такая функция найдена, необходимо задать уровень значимости j. Как правило, его величина берётся небольшой, чтобы доверительная вероятность P была как можно больше. Тогда построенный интервал обязательно будет включать истинное значение параметра. А также при построении графика учитывают, чтобы вероятность попадания вне интервала по обе стороны равнялись друг другу: (inf, S-(X|n|, j)), (S+(X|n|, j + inf).

Затем необходимо найти квантили статистики игрек порядка y (j/2) и y (1 — j/2). Исходя из определения квантили можно утверждать, что вероятность попадания статистики игрек в рассматриваемой интервале будет определяться разницей функции распределения соответствующих точек и равняться P = 1 — j. Описать это можно следующим выражением: P (y (j/2) < Y (S (X|n|), t) < y (1-j/2) = F (y (1-j/2) — F (y (j/2) = 1 — j.

Свойство статистики и распределения

Так как статистика по игреку строится таким образом, чтобы она была монотонной и непрерывной по тэте, то можно найти обратную функцию y^-1. Для определённости принимают, что игрек по тэта монотонно возрастает. Тогда вероятность расположения будет эквивалентна неравенству: y^-1(j/2) < t < y^-1(-j/2). Отсюда можно получить доверительный интервал для тэта: P (S -(X | n |, j) < t < S +(X | n |, j)) = 1 — j. Где: S -(X | n |, j) = Y^-1(y (a /2)), S +(X | n |, j) = Y^-1(y (1- a /2).

Таким образом, определить доверительную вероятность попадания тэта в интервал от S- до S+ можно от значения обратной функции в точках, равняющихся квантили статистики игрек порядка j/2 и 1 — j/2. При этом когда рассматриваемая функция монотонно убывает, знаки в неравенстве меняются на противоположные.

Пользуясь общим подходом расчёта доверительных интервалов, можно посчитать вероятность для нормальной генеральной совокупности, опираясь на ряд утверждений. Пусть известна выборка X|n,| взятая из совокупности E ~ N (j, ς²), то есть имеющей нормальный закон распределения с математическим ожиданием j и дисперсией сигма в квадрате. Для такого состояния справедливо следующее:

1. Функция вида (X-j) * √ n / ς соответствует стандартному нормальному закону распределения. Икс — это математическое ожидание неизвестного, из которого вычитается истинное значение для получения величины, имеющей нулевую вероятность. После этого величина центруется путём деления на среднее квадратичное отклонение: ς / √ n. Так как закон исходной генеральной совокупности нормальный, то и среднее арифметическое случайных величин будет являться нормально распределённой случайной величиной.
2. Если статистика S² не смещена от точки дисперсии, то функция (X — a) * √n / S будет подчиняться распределению Стьюдента с n — 1 степенью свободы.
3. Статистика n — 1, умноженная на несмещённый центр дисперсии и отнесённая к истинному значению, подчиняется распределению хи-квадрат. В числителе формулы находится сумма квадратов нормальных распределений, которые приводятся к нормальным стандартам.
4. Когда рассматривается смещённая оценка дисперсии, то статистика nS² / ς2 соответствует распределению хи-квадрат с эн степенями свободы.

Точный интервал

Существует ряд правил, позволяющих построить точные интервалы для математического ожидания и дисперсии нормально распределённой случайной величины. Есть два случая — при одном дисперсия может быть известной, а при другом нет. Следует обратить внимание, что точная доверительная вероятность строится с помощью общей схемы. Используют следующие правила для предоставления точных прогнозов:

1. При построении доверительного интервала с погрешностью 1 — E он определяется границами: P{ X — (ς / √n) * Z (1-E/2) и X + (ς / √n) * Z (1-E/2)}. Где: 1-E/2 — квантиль стандартного нормального распределения, которое симметричное.
2. Когда дисперсия неизвестна, в качестве оценки берётся несмещённая оценка S². Формула распределения в этом случае будет иметь вид: P{ X — (s / √n) * t (1-E/2) и X + (s / √n) * t (1-E/2)}. Значение t (1-E/2)} соответствует квантилю распределения Стьюдента с n — 1 свободной степенью.

Если ожидание неизвестно, то справедлива следующая формула: P {(n — 1) * s² / U (1- e /2) < ς² < (n — 1) * s ² / U (e /2) } = 1 — E. Доверительный интервал при известном j можно рассматривать как оценку математического ожидания: S² = 1/n Σ (xi-j)2, то есть равенство истинной дисперсии. Она с вероятностью 1 — E находится в интервале от n * S², делённая на квантиль распределения V (1-E/2) c уровнями свободы энной степени.

Измерение ожидания равняется истинной дисперсии, которая лежит в области от n * S², делённая на хи-квадрат с 1- E/2 степенью свободы, до n * S² с квантилей E /2. Если же ожидание неизвестно, в качестве дисперсии берётся несмещённая оценка S². При этом изменяется число степеней свободы хи-квадрат. Она становится n — 1. Всё остальное остаётся без изменений.

Асимптотическое приближение

Однако не всегда можно рассчитать точный доверительный интервал. В этом случае строится приближённая вероятность — асимптотическая. Пусть для некоторого j Є (0,1) существует набор статистик S-(X|n|, j) и S-(X|n|, j), причём такие, что lim P{ S-(X|n|, j) < t < S-(X|n|, j), } = 1- j, при эн, стремящемуся к бесконечности, тогда область, ограниченная интервалом (S-(X|n|, j), S-(X|n|, j)), является асимптотической приближённой. Её построение основывается на свойствах нормальных оценок. То есть для начала необходимо для параметра выбрать оценку, обладающую свойством асимптотической нормальностью.

Оценку тэты можно выполнить по формуле: t = t (x|n|), при этом √n (t-t) * (d / n → ∞) ~ N (0, ς2), а ς2 — коэффициент асимптотического рассеивания. Если делается несколько анализов одного параметра, то считается лучшим тот, у которого коэффициент будет меньше.

Применив теорему непрерывности к статистике, можно показать, что функция вида √n (t — t), отнесённая к среднестатистическому отклонению ς (t) по распределению, при n → ∞ сходится к случайной величине, имеющей стандартное распределение. То есть для последовательности случайных векторов справедливо выражение: kn = (k (n1), …, (k (nm). И если заданная функция непрерывна H: Rm →R, то H (k (n) * d / n → ∞, то имеет место сходимость: (√n (t — t) / ς (t)) / *(d / n → ∞) k ~ N (0, 1).

Отсюда будет справедливым следующее соотношение: P{-z (1-j/2) < z (1-j/2} → 1 — j = 1 / √2p ∫ (e -y2/2) dy. Таким образом, вероятность попадания будет находиться в области P є (z (1 — j/2), — z (1 — j/2)) и будет стремиться к минусу йод. Здесь z является квантилем 1- j/2. Точность интервальной оценки характеризуется шириной доверительной области. Чем больше объём выборки, тем уже будет рассматриваемый интервал (меньше ширина) и тем точнее будет интервальная оценка.

Примеры решения задач

Пусть имеется энное количество испытаний, из которых m являются успешными. Выборочный результат описывается функцией X|n| = (a1, …, an) и включает в себя нули и единицы. Статистика правдоподобия имеет вид: L (X|n|, p) = pm * q n-m, p є t = (0, 1). Для оценки правдоподобия необходимо составить функцию и найти оценки параметра P. Статистика имеет вид: ln L = mLnp + (n-m) ln (1-p). Максимальный результат выпадения единицы описывают выражением: d ln L / dP = (m / p) — (n — m) / (1 — p) = (m — mp -np + mp) / p (1 — p) = 0.

Отсюда получают оценку: p = m / n. Теперь нужно убедиться, что p максимизирует функцию правдоподобия. То есть d2LnL / dp2 = - m / p2 — (n — m) / (1 — p)2 < 0. Несложно доказать, что результат оценки будет асимптотически нормальным: √n ((m/n) — p) = (m -np) / √n = (Σ (ς i-p) / √n) (d / n → ∞) ~ N (0, pq). Воспользовавшись утверждением, довольно легко показать следующую сходимость: √n ((m/n) — p) / (√m/n (1 — m/n))) (d / n → ∞) ~ N (0, 1). Анализируя полученное, можно утверждать, что формула расчёта доверительного интервала будет иметь вид: ((m / n) — z (1-j/2) √m / n (1- m / n) / √n, (m / n + - z (1-j/2) √m / n (1- m / n) / √n)).

Более практичной является следующая задача. Пусть имеется предприятие, на котором решили узнать среднюю зарплату. В каких единицах она будет измеряться — значения не имеет. Для этого произвольно отобрали тридцать сотрудников, по анализу дохода которых выявили, что в месяц зарплата их составляет 30 тысяч с учётом среднего квадратичного отклонения в пять тысяч. Нужно рассчитать среднюю заработную плату за середину месяца с погрешностью менее 0,01 процента.

Сперва следует кратко записать условие. Известно, что n = 30, Xs = 30000, S = 5000, а P = 0,99. Для решения задачи необходимо использовать таблицу, соответствующую теореме Стьюдента. В ней собраны справочные величины для t — критерии с разной вероятностью. Согласно ей, для заданных значений n и P критерий равняется 2,756.

Подставив исходные данные в формулу и выполнив вычисления, можно утверждать, что необходимая доверительная область ограничивается интервалом от 27484 до 32516: 30000 — 2,756 * (5000 / √30) < Xs < 3000 + 2,756 * (5000 / √30). То есть средняя зарплата сотрудников за половину месяца лежит в интервале (13742, 16258). Задача решена.

Использование онлайн-калькулятора

На практике довольно часто вычислить доверительную область не так уж и просто. Всё дело в том, что высокая вероятность часто находится в выборке большого объёма, поэтому приходится выполнять громоздкие вычисления. Учитывая, что доверительная вероятность определяет точность полученных результатов, другими словами, показывает, с какой вероятностью неправильное решение попадает в найденный интервал, обычно используют процент выборки от 95 до 99,9%.

Для высокой точности получения диапазона как раз и используют сервисы, которые в последнее время начали называться онлайн-калькуляторами. Это специализированные сайты, умеющие в автоматическом режиме решать различные математические задания. Особенность этих сайтов в том, что они предоставляют услуги бесплатно, при этом от их пользователей не требуется никаких знаний.

Всё что им нужно — это ввести в пролагаемую форму данные и нажать кнопку «Рассчитать». Система автоматически вычислит ответ и выведет его на экран. Из наиболее популярных можно отметить следующие сервисы:

1. Webstarstudio.
2. MathSemestr.
3. Allcalc.

Они доступны на русском языке, их интерфейс интуитивно понятен, поэтому воспользоваться их услугами сможет любой заинтересованный, имеющий доступ к интернету. Автоматический расчёт занимает буквально секунды, что составляет существенную разность по сравнению с затратой времени при самостоятельном вычислении.