Содержание:

Определение шара и его радиуса

Начнем с главных определений:

Шар (сфера) - это совокупность точек трехмерного пространства, находящихся на расстоянии свыше заданного от центра. В повседневной жизни мы постоянно встречаемся с данной формой. В обыденности мы даже не замечаем на сколько масштабно присутствие фигуры рядом с нами, вне зависимости от того, какое будет наше местонахождение.

Часто путают объемную формой и круг. Конкретнее различать их помогут знания о том, что один является объемной фигурой, а другой плоской. Разберем визуально: стол - он круглый, так как имеет свою плоскость и никак не может приобрести объем, а если сможет, то потеряет свою основную функцию - возможность что-то поставить и удержать на месте; теперь возьмем мяч - это полноценная сфера, ведь он объемный, благодаря чему, способен катиться по поверхности при малейшем движении.

Радиус шара - отрезок, соединяющий точку поверхности с центром. Его длина имеет такое же название. Соответственно, этим определением можно называть как отрезок, так и длину отрезка (число).

Так можно найти:

  1. Площадь поверхности.

  2. Площадь сечения.

  3. Объем геометрической фигуры.

радиус шара равен

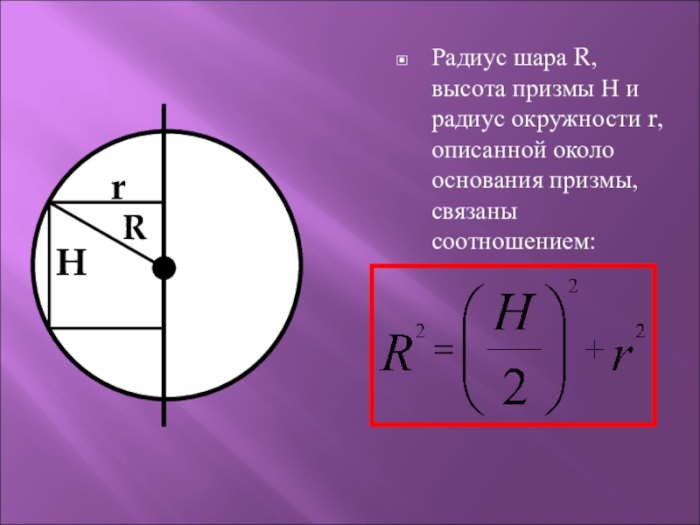
Формулы для вычислений

Радиус по диаметру находится по формуле:

r= D/2, где D - диаметр.

Примеры:

1. Если диаметр сферы составляет 22 см, то:

r = 22/2=12

2. При диаметре 48 см:

r = 48/2=24

3. Диаметр шара - 17,2 см, его радиус составит:

17,2/2=8,6

Радиус по длине окружности вычисляется по формуле:

r = C/2π, где С - длина окружности, а п - число Пи (3,14).

Примеры:

1. Если периметр круга 28 см, то:

r = 28/2*3,14=4,458

2. Периметр круга 36 мм, тогда радиус шара равен:

r = 36/2*3,14= 5,732

3. Если длина окружности 42,2 см, тогда:

r = 42,2/2*3,14=6,719

Данные формулы действительны как для сферы, так и круга.