Обыкновенные дроби в математике
\( \frac{1}{12} \)
Содержание:
Не всегда людям приходится иметь дело с целыми числами, обыкновенные дроби также надо знать каждому. Даже если вы не математик, постоянно возникает необходимость то отгородить одну четверть участка, то разрезать фрукт или пирог, чтобы досталось всем поровну, то прибавить к пятой части стакана крупы еще осьмушку. Во всех этих случаях вы, сами того не желая, вспоминаете, что же такое обыкновенные дроби и как с ними обращаться.
Если вы пишете в тетрадке, вам удобнее записать дробь в столбик. Снизу указывают, с какими долями вы имеете дело, сверху – сколько их взяли, а между ними ставится горизонтальная черта: \( \frac{4}{7} \) ,\( \frac{5}{8} \) ,\( \frac{13}{25} \). Теперь давайте разберемся, как называется каждый элемент этой комбинации:
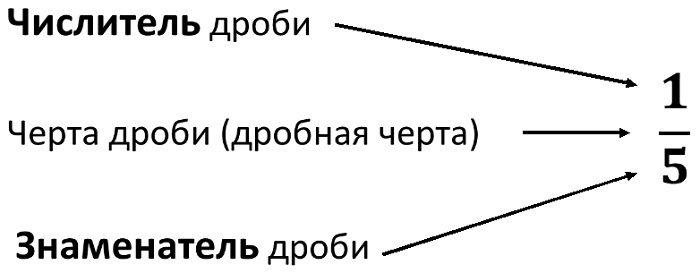
Рис. 1 Обозначения элементов обыкновенной дроби Дроби бывают очень странными! Например, вы видите в задачнике такую - \( \frac{15}{1} \). Удивляться не надо. В обычных-то случаях то, что написано внизу, больше. И это правильные дроби. А если наоборот, как в последнем примере, или же элементы одинаковые - неправильные.

Рис. 2 Правила сравнения дробей
Разбираемся с долями
Допустим, вас в компании трое, и у вас есть всего один банан. Как сделать, чтобы никому не было обидно и всем досталось хотя бы понемногу? Это очень просто – всего-то и нужно, что разрезать фрукт на три абсолютно одинаковые части. Банан был целый, а вот то, что достанется каждому, будет считаться его долей. Еще нагляднее, если у вас есть что-то, что сразу делится на частички. Пусть будет мандарин. Каждая его долька является частью целого. Давайте не будем его есть сразу, а посчитаем, сколько было частиц. Например, 12. Тогда каждая их них является от единицы, то есть от мандарина. С бананом - то же самое. Целый - 1, а каждый кусочек, который мы отрезали - \( \frac{1}{3} \). Вот мы и получили две обыкновенные дроби – и \( \frac{1}{3} \). А что будет, если, к примеру, кто-то возьмет не одну треть от банана, а две? Или, скажем, каждому перепадет по 2 или 3 мандариновых дольки? Тогда мы так и запишем: Пете досталось \( \frac{2}{3} \) банана, или \( \frac{2}{12} \) мандарина, а то даже и \( \frac{3}{12} \).Как называются части?
В некоторых случаях доли называются так, как они записаны – например, та же самая никак, кроме одной двенадцатой, и не именуется. А вот \( \frac{1}{2} \) имеет свое особое название – половина. От банана каждому досталась треть. Если бы в комнате было четыре человека, каждому перепало бы по четверти. Для того чтобы определить, какие имеются в виду частицы и сколько их, и применяются обыкновенные дроби. И, конечно, мы всегда можем обозначить буквами и то, и другое.Важно! Очень часто доли целого применяются в метрических системах. Например, сантиметр – это сотая доля метра, или \( \frac{1}{100} \).
Поговорим об элементах
- Верхнее число называется числителем – оно указывает на число долей.
- Нижнее – знаменатель, по нему мы узнаем, на сколько равных кусков разбили то, что считается единицей.

Зачем нужна черта?
Если мы делим один предмет на несколько частей, в правой части будет стоять единичка. А если у нас 3 авокадо, а разделить нужно на четверых, что тогда? Тогда, хочешь не хочешь, придется считать. Со знаменателем все понятно, делить надо на четверых. А как быть с числителем? Пишем количество целых фруктов, то есть 3. В итоге получается, что каждому достанется \( \frac{3}{4} \). А если количество авокадо мы запишем как a, а количество людей – как b, дробь будет выглядеть как \( \frac{a}{b} \), и подставить можно любые числа. А черточка – это и есть знак деления, который заменяет и традиционные точки, и уголок. Просто так удобнее.Сравниваем дроби
Со сравнением целых чисел все понятно - там видно, какое больше, а какое меньше. А как быть с дробными? Ничто не мешает сравнить и их. Если, к примеру, мы разделили что-то на 6 частей, и кому-то досталась \( \frac{1}{6} \), а кому-то - \( \frac{3}{6} \), то всем понятно, что 3 больше одного. То есть из двух дробей с одинаковой нижней частью больше будет та, у которой больше верхняя. Когда каждый взял по \( \frac{2}{6} \), тоже ясно, что всем поровну и никто не в обиде. И числители, и знаменатели одинаковы, значит, и дроби тоже равны.
Внизу - разные числа
Иногда сравнить дроби бывает довольно трудно – именно те, у которых разные знаменатели. В этом случае практикуется приведение к общему знаменателю, без него просто никак не обойтись. Например, давайте попробуем сравнить \( \frac{2}{3} \) и \( \frac{3}{4} \). Как это сделать? Надо найти такое число, которое делится на обе нижние части. Причем это должно быть самое маленькое из всех возможных. Это число 12. В обоих дробях пишем его в знаменатель \( \frac{a}{12} \) и \( \frac{b}{12} \). Да, но что при этом делать с числителем? Ведь ясно, что его нельзя оставлять так, как есть – сначала были у нас треть и четверть, а теперь стала двенадцатая часть. Для этого верхние части дробей умножим на столько же, на сколько и нижние. Получим соответственно \( \frac{8}{12} \) там, где было две трети, и \( \frac{9}{12} \) вместо трех четвертей. Остается сравнить, какой числитель больше. Как видите, обыкновенные дроби очень полезны, и надо в них разобраться. Но это не является сложной темой, если один раз хорошенько вникнуть что к чему. Для наглядности предлагаем вам посмотреть еще и видео, где вы найдете больше примеров по этой теме. >Все тесты
- Английский язык
- Биология
- История
- Физкультура
- Пушкин А.С
- Религия
- Карьера
- Информатика
- Физика
- Стихи
- Обществознание
- Сочинения
- ОБЖ
- Экономика
- Подготовка к ЕГЭ
- Помощь студенту
- География
- Математика
- Пунктуация
- Правоведение
- Орфография
- Анализ стихотворений
- Краткие содержания
- Биографии
- Литература
- Русский язык
- Окружающий мир
- Фонетический разбор
- Тест на тему To be going to: значение, правила употребления 5 вопросов
- Тест на тему Конструкция go on: значения, правила употребления, примеры 5 вопросов
- Тест на тему Be familiar with: значение и правила употребления 5 вопросов
- Тест на тему Британский vs американский английский: в чем разница? 5 вопросов
- Тест на тему Be mad about - как переводится и как использовать в речи 5 вопросов
- Тест на тему Be hooked on в английском языке: значение и примеры предложений 5 вопросов
- Тест на тему «To be made» в английском языке: значение, правила и примеры для школьников 5 вопросов
- Тест на тему Приставки in-, im-, il-, ir- в английском языке: полный разбор для школьников 5 вопросов
- Тест на тему «To be given» в английском языке: значение, употребление и примеры для школьников 5 вопросов
- Тест на тему Подборка интересных фактов про английский язык 5 вопросов
- Тест на тему История сибирской язвы и как она стала оружием 5 вопросов
- Тест на тему Что такое “железное легкое” и как жилось узникам аппарата 5 вопросов
- Тест на тему Суть и методы клеточной инженерии 5 вопросов
- Тест на тему Злаковые растения - общая характеристика, признаки и список представителей 7 вопросов
- Тест на тему Семейство бобовые - общая характеристика, строение и представители 7 вопросов
- Тест на тему Команда реформ: сподвижники Петра I 10 вопросов
- Тест на тему Экономика и управление: реформы Афанасия Ордина-Нащокина 10 вопросов
- Тест на тему Положение крестьян и указ Павла I о трехдневной барщине 10 вопросов
- Тест на тему Программа Южного общества и декабрист П. И. Пестель 10 вопросов
- Тест на тему Комитет общественного блага или Негласный комитет 10 вопросов
- Тест на тему Планы переустройства России: «Конституция» Муравьева 10 вопросов
- Тест на тему Характеристика «золотого века» российского дворянства 10 вопросов
- Тест на тему Содержание греческого проекта императрицы Екатерины II 10 вопросов
- Тест на тему Причины и ход денежной реформы Е. Ф. Канкрина 10 вопросов
- Тест на тему Как работал дворянский заемный банк 10 вопросов
- Тест на тему История и судьба владельческих крестьян 10 вопросов
- Тест на тему История битвы при Добрыничах 1605 года 10 вопросов
- Тест на тему 10 сталинских ударов: как Красная армия освободила Европу в 1944 году 10 вопросов
- Тест на тему Красный и белый террор в годы Гражданской войны 5 вопросов
- Тест на тему История появления имущественного неравенства и знати 5 вопросов
- Тест на тему Народы, населявшие Россию во второй половине 16 века 5 вопросов
- Тест на тему Первые государства: история образования и функции 5 вопросов
- Тест на тему Роль огня в жизни первобытных и современных людей 5 вопросов
- Тест на тему 5 самых известных разведчиков в истории 5 вопросов
- Тест на тему Присоединение к Московскому государству Смоленска 5 вопросов
- Тест на тему Причины и предпосылки объединения русских земель вокруг Москвы 5 вопросов
- Тест на тему Формирование русского централизованного государства 5 вопросов
- Тест на тему Краткая история Руси в 15 веке: главные события, культура 5 вопросов
- Тест на тему Причины и итоги установления автокефалии Русской Церкви 5 вопросов
- Тест на тему Особенности общественного строя и церковной организации на Руси 5 вопросов
- Тест на тему Когда появились первые известия о русских и Руси? 5 вопросов
- Тест на тему Призвание на княжение в Новгород варягов 5 вопросов
- Тест на тему История присоединения Псковского княжества к Московскому 5 вопросов
- Тест на тему История битв при Чашниках в 1564 и 1657 годах 5 вопросов
- Тест на тему Правление Василия 1 Дмитриевича 5 вопросов
- Тест на тему Земская реформа Ивана Грозного 5 вопросов
- Тест на тему Все князья Московского княжества 5 вопросов
- Тест на тему Причины, ход восстания Тадеуша Костюшко и его итоги 5 вопросов
- Тест на тему Последствия Смутного времени в России 5 вопросов
- Тест на тему Главные реформы короля Священной Римской империи Иосифа 2 5 вопросов
- Тест на тему Состав и функции государева двора 5 вопросов
- Тест на тему Суть “дела Дрейфуса” и реакция общества 5 вопросов
- Тест на тему Деятельность партии монтаньяров во Франции 5 вопросов
- Тест на тему Традиции и обычаи украинского народа 5 вопросов
- Тест на тему Причины закрытия Японии в 17 веке и последствия 5 вопросов
- Тест на тему Подготовка и содержание генерального плана “Ост” 5 вопросов
- Тест на тему Тайны убийства Петра Столыпина 5 вопросов
- Тест на тему Отмена подушной подати на Руси 5 вопросов
- Тест на тему Период регентства Елены Глинской: события и реформы 5 вопросов
- Тест на тему Экономика России в годы Первой мировой войны 5 вопросов
- Тест на тему Битва при деревне Лесной 28 сентября 1708 года 5 вопросов
- Тест на тему 10 любопытных фактов про Рождество 5 вопросов
- Тест на тему 10 любопытных фактов про Новый год 5 вопросов
- Тест на тему История потешных полков Петра Первого 5 вопросов
- Тест на тему Образование и распад тушинского лагеря при Лжедмитрии II 5 вопросов
- Тест на тему Реферат по физкультуре на тему: «Здоровое питание» 5 вопросов
- Тест на тему История развития лыжного спорта в разных странах - классификация и интересные факты 6 вопросов
- Тест на тему Важность самоконтроля при занятиях спортом 5 вопросов
- Тест на тему Как выполняются прыжки через козла? 5 вопросов
- Тест на тему Что такое здоровый образ жизни? 5 вопросов
- Тест на тему Как правильно выполнять кувырки? 5 вопросов
- Тест на тему Развитие гибкости тела: упражнения и польза для тела 5 вопросов
- Тест на тему Виды и польза прыжков через скакалку 5 вопросов
- Тест на тему Какие есть зимние виды спорта? 5 вопросов
- Тест на тему Реферат на тему: “Гимнастика как вид спорта” 8 вопросов
- Тест на тему Реферат по физкультуре на тему “Футбол” 7 вопросов
- Тест на тему Реферат по физкультуре на тему: “Баскетбол - виды и лиги” 7 вопросов
- Тест на тему Реферат на тему «Лыжный спорт» 10 вопросов
- Тест на тему Реферат по физической культуре «Формы и виды закаливания» 10 вопросов
- Тест на тему Образ Шарикова в повести «Собачье сердце» М. Булгакова 5 вопросов
- Тест на тему Образы героев в повести «Невский проспект» Н. Гоголя 5 вопросов
- Тест на тему Московские главы в романе «Мастер и Маргарита» Булгакова 7 вопросов
- Тест на тему Описание образа бирюка из рассказа И. Тургенева 7 вопросов
- Тест на тему Образы героев в романе «Отцы и дети» И. Тургенева 7 вопросов
- Тест на тему Образы героев в повести «Котлован» А. Платонова 7 вопросов
- Тест на тему Образы героев в пьесе «Гроза» А. Островского 7 вопросов
- Тест на тему История создания повести Н. В. Гоголя “Шинель” 7 вопросов
- Тест на тему История создания сборника рассказов Тургенева “Записки охотника” 7 вопросов
- Тест на тему История создания повести "Муму" Ивана Тургенева 7 вопросов
- Тест на тему История создания стихотворения "Реквием" Анны Ахматовой 10 вопросов
- Тест на тему История создания повести Гоголя "Тарас Бульба" 10 вопросов
- Тест на тему История создания стихотворения Пушкина "Деревня" 6 вопросов
- Тест на тему История создания стихотворения М. Лермонтова “Нищий” 7 вопросов
- Тест на тему История создания стихотворения "Она сидела на полу" 7 вопросов
- Тест на тему История создания Пушкиным стихотворения "К морю" 6 вопросов
- Тест на тему История создания повести «Станционный смотритель» А. Пушкина 10 вопросов
- Тест на тему История создания «Оды на день восшествия» М. Ломоносова 7 вопросов
- Тест на тему Что нужно сдавать на бухгалтера? 5 вопросов
- Тест на тему Какие предметы нужно сдавать на пилота 5 вопросов
- Тест на тему Какие экзамены нужно сдавать на фотографа? 5 вопросов
- Тест на тему Какие предметы нужно сдавать на хореографа? 5 вопросов
- Тест на тему Какие предметы нужно сдавать на актера? 5 вопросов
- Тест на тему Какие предметы нужно сдавать на режиссера? 5 вопросов
- Тест на тему Что нужно сдавать на художника? 5 вопросов
- Тест на тему Что нужно сдавать для поступления на визажиста? 5 вопросов
- Тест на тему Какие экзамены нужно сдавать на полицейского? 5 вопросов
- Тест на тему Какие предметы нужно сдавать на фармацевта? 5 вопросов
- Тест на тему Какие предметы сдавать для поступления на врача? 5 вопросов
- Тест на тему Какие экзамены нужно сдавать на учителя 5 вопросов
- Тест на тему Кадетский корпус - как поступить, чему учат и условия для проживания 5 вопросов
- Тест на тему Готовы ли вы к поступлению на психолога? 5 вопросов
- Тест на тему Готовы ли вы к поступлению на дизайнера? 5 вопросов
- Тест на тему Острова и полуострова Зарубежной Европы 10 вопросов
- Тест на тему Уровень урбанизации Африки: города растут, вызовы множатся 5 вопросов
- Тест на тему Уровень и особенности урбанизации Канады 5 вопросов
- Тест на тему Как найти полярную звезду и зачем ее искать? 5 вопросов
- Тест на тему Что нужно знать про контурные карты 5 вопросов
- Тест на тему Кто, когда и как открыл Австралию? 5 вопросов
- Тест на тему Характеристика природных зон Поволжья 5 вопросов
- Тест на тему Для каких рек в России характерно летнее половодье? 5 вопросов
- Тест на тему Как правильно заполнять дневник наблюдения за погодой 5 вопросов
- Тест на тему Влажные экваториальные леса - особенности климата, характеристика флоры и фауны 7 вопросов
- Тест на тему Европейский север России - географическое положение, особенности развития предприятий и промышленности 7 вопросов
- Тест на тему Что такое масштаб карты и как его определять 7 вопросов
- Тест на тему Особенности и примеры островных государств 5 вопросов
- Тест на тему Природные зоны Южной Америки - характеристики и особенности 7 вопросов
- Тест на тему 10 интересных фактов про океан 7 вопросов
- Тест на тему Сектор Газа: где он находится и откуда такое название? 6 вопросов
- Тест на тему Особенности раздельного написания местоимений с предлогами 5 вопросов
- Тест на тему Правописание падежных окончаний прилагательных 5 вопросов
- Тест на тему Правописание слов с непроверяемой безударной гласной в корне 5 вопросов
- Тест на тему Нужно ли ставить запятую к фразе - "с уважением"? 5 вопросов
- Тест на тему «Во-вторых» или «во вторых» – как правильно пишется? 5 вопросов
- Тест на тему "Нету" или "нет" - как правильно писать и говорить? 5 вопросов
- Тест на тему «Не я» или «нея» – как правильно пишется? 5 вопросов
- Тест на тему «Полным-полно» или «полным полно» - как правильно пишется? 5 вопросов
- Тест на тему Как пишется «кто-нибудь» или «кто нибудь»? 5 вопросов
- Тест на тему Мягкий знак после шипящих в глаголах - правила, примеры 5 вопросов
- Тест на тему «Потвёрже» или «по твёрже» – как правильно пишется? 5 вопросов
- Тест на тему «Какой-то» или «какой то» – как пишется правильно? 5 вопросов
- Тест на тему «Мало-помалу» или «мало помалу» – как правильно пишется? 5 вопросов
- Тест на тему «По-осеннему» или «по осеннему» – как правильно пишется? 5 вопросов
- Тест на тему "Находу" или "на ходу" - слитно или раздельно писать? 5 вопросов
- Тест на тему "ЮлИчка" или "ЮлЕчка" - как правильно писать? 5 вопросов
- Тест на тему «Не пойму» или «непойму» – как правильно пишется? 5 вопросов
- Тест на тему «Доброе утро» − как правильно пишется? 5 вопросов
- Тест на тему «Почему-то» или «почему то» – как правильно пишется? 5 вопросов
- Тест на тему «На вынос» или «навынос» – как правильно пишется? 5 вопросов
- Тест на тему «Невежливо» или «не вежливо» – как правильно пишется? 5 вопросов
- Тест на тему «Негодуя» или «не годуя» - как правильно пишется? 5 вопросов
- Тест на тему «КуриНый» или «куриННый» − как правильно пишется? 5 вопросов
- Тест на тему «ТеННис» или «теНис» – как правильно пишется? 5 вопросов
- Тест на тему «ТумаННый» или «тумаНый» – как правильно пишется? 5 вопросов
- Тест на тему «ЗамечеННый» или «замечеНый» – как правильно пишется? 5 вопросов
- Тест на тему «Семнадцать» или «семЬнадцать» – как правильно пишется? 5 вопросов
- Тест на тему «ВыздОравливающий» или «выздАравливающий» – как правильно пишется? 5 вопросов
- Тест на тему «Свеж» или «свежЬ» – как правильно пишется? 5 вопросов
- Тест на тему «СлаЩе» или «слаДЧе» – как правильно пишется? 5 вопросов
- Тест на тему «ПрЕтерпевать» или «прИтерпевать» - как правильно пишется? 5 вопросов
- Тест на тему «Удастся» или «удастЬся» – как правильно пишется? 5 вопросов
- Тест на тему «СписаНо» или «СписаННо» – как правильно пишется? 5 вопросов
- Тест на тему «Происшествие» или «проишествие» – как правильно пишется? 5 вопросов
- Тест на тему «НачИнающий» или «начЕнающий» – как правильно пишется? 5 вопросов
- Тест на тему «Невозможно» или «не возможно» – как пишется слитно или раздельно? 5 вопросов
- Тест на тему «Налету» или «на лету» – как правильно пишется? 5 вопросов
- Тест на тему «Надолго» или «на долго» – как правильно пишется? 5 вопросов
- Тест на тему «ПьющАя» или «пьющЕя» – как правильно пишется? 5 вопросов
- Тест на тему «Неужели» или «не ужели» − как правильно пишется? 5 вопросов
- Тест на тему «НИкого» или «нЕкого» – как правильно пишется? 5 вопросов
- Тест на тему «БаССейн» или «баСейн» − как правильно пишется? 5 вопросов
- Тест на тему "Не согласованно" или "несогласованно" - слитно или раздельно? 5 вопросов
- Тест на тему «ОбстОятельствам» или «обстАятельствам» – как правильно пишется? 5 вопросов
- Тест на тему «ОбижеННый» или «обижеНый» – как правильно пишется? 5 вопросов
- Тест на тему «Аллах» или «Алах» – как правильно пишется? 5 вопросов
- Тест на тему «БелОрусский» или «белАрусский» – как правильно пишется? 5 вопросов
- Тест на тему «ЧИсло» или «чЕсло» – как правильно пишется? 5 вопросов
- Тест на тему «УвЕряющий» или «увИряющий» – как правильно пишется? 5 вопросов
- Тест на тему «НенасТный» или «ненасный» – как правильно пишется? 5 вопросов
- Тест на тему Анализ стихотворения “Каким бы малым ни был...” К. Кулиева 5 вопросов
- Тест на тему Анализ стихотворения «Цицерон» Ф. Тютчева 5 вопросов
- Тест на тему Анализ стихотворения “Поэт” М. Лермонтова 5 вопросов
- Тест на тему Анализ стихотворения “Пора, мой друг, пора” А. Пушкина 5 вопросов
- Тест на тему Анализ стихотворения «Шестое чувство» Н. Гумилева 5 вопросов
- Тест на тему Анализ стихотворения “Юбилейное” В. Маяковского 5 вопросов
- Тест на тему Анализ стихотворения “Мой гений” К. Батюшкова 5 вопросов
- Тест на тему Анализ стихотворения «Нет, не тебя так пылко» М. Лермонтова 5 вопросов
- Тест на тему Анализ стихотворения «Догорел апрельский светлый вечер…» И. Бунина 5 вопросов
- Тест на тему Анализ стихотворения «Фонтан» Ф. Тютчева 5 вопросов
- Тест на тему Анализ стихотворения «Посмотри - какая мгла» Я. Полонского 5 вопросов
- Тест на тему Анализ стихотворения «Школьник» Н. Некрасова 5 вопросов
- Тест на тему Анализ стихотворения «Несжатая полоса» Н. Некрасова 5 вопросов
- Тест на тему «Весенний дождь» - анализ стихотворения А.А. Фета 7 вопросов
- Тест на тему «Поет зима - аукает» - анализ стихотворения С.А. Есенина 7 вопросов
- Тест на тему Краткое содержание повести «А тем временем где-то» А. Алексина 5 вопросов
- Тест на тему Краткое содержание комедии «Мнимый больной» Жана-Батиста Мольера 5 вопросов
- Тест на тему Краткое содержание комедии “Доходное место” А. Островского 5 вопросов
- Тест на тему Краткое содержание новеллы “Падение дома Ашеров” Эдгара По 5 вопросов
- Тест на тему Краткое содержание рассказа “Крепкий мужик” В. Шукшина 5 вопросов
- Тест на тему Краткое содержание пьесы «Золотая карета» Л. Леонова 5 вопросов
- Тест на тему Краткое содержание рассказа «Когда в доме одиноко» К. Саймака 5 вопросов
- Тест на тему Краткое содержание рассказа “Простите нас” Ю. Бондарева 5 вопросов
- Тест на тему Краткое содержание романа “Кысь” Т. Толстой 5 вопросов
- Тест на тему Краткое содержание повести “Это мы, Господи!” К. Воробьева 5 вопросов
- Тест на тему Краткое содержание романа «Как закалялась сталь» Н. Островского 5 вопросов
- Тест на тему Краткое содержание романа-эпопеи «Хождение по мукам» А. Толстого 5 вопросов
- Тест на тему Краткое содержание сказки “Журавль и цапля” 5 вопросов
- Тест на тему Краткий пересказ “О чем говорят цветы” Жорж Санд 5 вопросов
- Тест на тему Краткое содержание рассказа “Тринадцать лет” С. Баруздина 5 вопросов
- Тест на тему Краткое содержание рассказа «Парадокс» В. Короленко 5 вопросов
- Тест на тему Краткое содержание романа «Живые и мертвые» К. Симонова 5 вопросов
- Тест на тему Краткое содержание повести «Обмен» Юрия Трифонова 5 вопросов
- Тест на тему Краткое содержание рассказа “Алешкино сердце” М. Шолохова 5 вопросов
- Тест на тему Краткое содержание рассказа “Как я стал писателем” И. Шмелева 5 вопросов
- Тест на тему Краткое содержание рассказа “Гамбринус” А. Куприна 5 вопросов
- Тест на тему Краткое содержание сказки “Вафельное сердце” Марии Парр 5 вопросов
- Тест на тему Краткое содержание рассказа “Специалист” А. Аверченко 5 вопросов
- Тест на тему Краткое содержание пьесы «Трамвай “Желание”» Т. Уильямса 5 вопросов
- Тест на тему Краткое содержание романа “Война миров” Г. Уэллса 5 вопросов
- Тест на тему Краткое содержание рассказа “Баргамот и Гараська” Л. Андреева 5 вопросов
- Тест на тему Краткое содержание повести “Скотный двор” Д. Оруэлла 5 вопросов
- Тест на тему «Акула» Л. Толстого - краткое содержание 5 вопросов
- Тест на тему Русская народная сказка «Хвосты» - краткое содержание 5 вопросов
- Тест на тему Краткое содержание оперы «Снегурочка» Римского-Корсакова 5 вопросов
- Тест на тему «Обезьяний язык» М. Зощенко – краткое содержание 10 вопросов
- Тест на тему «Сердце не камень» - краткое содержание пьесы А.Н. Островского 5 вопросов
- Тест на тему Балет «Щелкунчик» — краткое содержание 7 вопросов
- Тест на тему Биография Владимира Вольфовича Жириновского 5 вопросов
- Тест на тему Биография поэта и писателя Льва Рубинштейна 5 вопросов
- Тест на тему Биография президента Белоруссии Александра Лукашенко 5 вопросов
- Тест на тему 10 интересных фактов про Афанасия Фета 5 вопросов
- Тест на тему 10 интересных фактов про Ивана Тургенева 5 вопросов
- Тест на тему Биография писателя и поэта Вячеслава Урюпина 5 вопросов
- Тест на тему Биография поэта Николая Михайловича Рубцова 5 вопросов
- Тест на тему Биография поэта Андрея Дмитриевича Дементьева 5 вопросов
- Тест на тему Биография президента РФ Владимира Путина 5 вопросов
- Тест на тему Биография и личная жизнь Даниила Хармса 5 вопросов
- Тест на тему Краткая биография Валентины Осеевой 5 вопросов
- Тест на тему Григорий Остер: биография писателя и избранные произведения 7 вопросов
- Тест на тему Елена Благинина: творческая биография и личная жизнь 10 вопросов
- Тест на тему Биография детской писательницы Ирины Пивоваровой 5 вопросов
- Тест на тему История создания рассказа «Матренин двор» А. Солженицына 5 вопросов
- Тест на тему История создания песни «Смуглянка» 5 вопросов
- Тест на тему История создания поэмы “Кому на Руси жить хорошо” Н. Некрасова 5 вопросов
- Тест на тему История создания романа “Как закалялась сталь” Н. Островского 5 вопросов
- Тест на тему История создания оперы М. Глинки «Иван Сусанин» 5 вопросов
- Тест на тему История создания знаменитой песни “Катюша” 5 вопросов
- Тест на тему История создания поэмы “За далью - даль” А. Твардовского 5 вопросов
- Тест на тему История создания стихотворения “Смерть поэта” М. Лермонтова 5 вопросов
- Тест на тему История создания рассказа “Кавказский пленник” Л. Н. Толстого 5 вопросов
- Тест на тему История создания песни Р. Гамзатова “Журавли” 5 вопросов
- Тест на тему История создания стихотворения “Зимнее утро” А. С. Пушкина 5 вопросов
- Тест на тему История создания рассказа "Судьба человека" М. Шолохова 5 вопросов
- Тест на тему История создания стихотворения "На холмах Грузии лежит ночная мгла..." А. Пушкина 5 вопросов
- Тест на тему История создания романа “Идиот” Ф. М. Достоевского 5 вопросов
- Тест на тему История создания рассказа «Васюткино озеро» В. Астафьева 5 вопросов
- Тест на тему История создания повести “Детство” Л. Толстого 5 вопросов
- Тест на тему История создания романа «Дон Кихот» М. Сервантеса 5 вопросов
- Тест на тему История создания романа «Бесы» Ф. Достоевского 5 вопросов
- Тест на тему История создания романа «Молодая гвардия» А. Фадеева 5 вопросов
- Тест на тему История создания пьесы «Моцарт и Сальери» А. С. Пушкина 5 вопросов
- Тест на тему История создания баллады «Лесной царь» Ф. Шуберта 5 вопросов
- Тест на тему "Миссия русской эмиграции" И. Бунина 5 вопросов
- Тест на тему История создания пьесы «Бесприданниц» А. Островского 5 вопросов
- Тест на тему История создания повести “Алые паруса” А. Грина 1 вопрос
- Тест на тему История создания романа “Бедные люди” Ф. Достоевского 5 вопросов
- Тест на тему Герои романа “Властелин колец” Д. Толкина 5 вопросов
- Тест на тему Анализ сказа “Серебряное копытце” П. Бажова 5 вопросов
- Тест на тему Характеристика Дуняши в романе “Тихий Дон” М. Шолохова 5 вопросов
- Тест на тему Описание образа Фамусова - персонажа комедии “Горе от ума” 5 вопросов
- Тест на тему Характеристика образа Сатина - персонажа пьесы “На дне” М. Горького 5 вопросов
- Тест на тему Анализ повести “Сашка” В. Кондратьева 5 вопросов
- Тест на тему Характеристика образа Фауста из трагедии Гёте 9 вопросов
- Тест на тему Анализ романа “Портрет Дориана Грея” О. Уайльда 5 вопросов
- Тест на тему Характеристика колобка - героя русской народной сказки 5 вопросов
- Тест на тему Образ главной героини “Алисы в стране чудес” Л. Кэррола 5 вопросов
- Тест на тему Трактовки образа Иисуса Христа в поэме “Двенадцать” А. Блока 5 вопросов
- Тест на тему Образ Настеньки из повести “Белые ночи” Ф. Достоевского 5 вопросов
- Тест на тему Конфликт в рассказе “После бала” Л. Толстого 5 вопросов
- Тест на тему Образ главной героини повести “Бедная Лиза” Н. Карамзина 5 вопросов
- Тест на тему Описание образа Васютки из рассказа “Васюткино озеро” В. Астафьева 5 вопросов
- Тест на тему Образы чиновников в комедии “Ревизор” Н. Гоголя 5 вопросов
- Тест на тему Роль образа вишневого сада в пьесе А. Чехова 5 вопросов
- Тест на тему Характеристика профессора Преображенского в повести “Собачье сердце” М. Булгакова 5 вопросов
- Тест на тему Описание образа городничего в комедии “Ревизор” Н. Гоголя 5 вопросов
- Тест на тему Описание образа главного героя “Доктора Живаго” Б. Пастернака 5 вопросов
- Тест на тему Образ Цыганка в повести “Детство” М. Горького 5 вопросов
- Тест на тему Характеристика Вани Солнцева в повести “Сын полка” В. Катаева 5 вопросов
- Тест на тему Образ автора в поэме "Василий Теркин" А. Твардовского 5 вопросов
- Тест на тему Образ портрета в повести "Портрет" Н. В. Гоголя 5 вопросов
- Тест на тему Описание образа девушки-ундины из “Героя нашего времени” М. Лермонтова 5 вопросов
- Тест на тему Как выполнить разбор наречия по составу 5 вопросов
- Тест на тему Правила правописания суффиксов наречий 5 вопросов
- Тест на тему Морфологический признак наречий: неизменяемость 5 вопросов
- Тест на тему Чем отличаются и как найти тему и рему в тексте? 5 вопросов
- Тест на тему Способы и примеры образования наречий 5 вопросов
- Тест на тему Особенности и применение составных предлогов 5 вопросов
- Тест на тему Какую синтаксическую роль в предложении выполняет наречие 5 вопросов
- Тест на тему Какие признаки прилагательного есть у причастия 5 вопросов
- Тест на тему Морфологический разбор союзов: инструкция, примеры 5 вопросов
- Тест на тему Морфологические признаки действительных и страдательных причастий 5 вопросов
- Тест на тему Особенности и примеры звукоподражательных слов 5 вопросов
- Тест на тему Какие бывают и как определить смысловую группу наречий 5 вопросов
- Тест на тему Неправильное построение предложений с косвенной речью: примеры ошибок 5 вопросов
- Тест на тему Расстановка знаков препинания в сложноподчиненных предложениях 5 вопросов
- Тест на тему Виды синтаксических связей в словосочетаниях и предложениях 5 вопросов
- Тест на тему Оформление и примеры несобственно-прямой речи в тексте 5 вопросов
- Тест на тему Структура текста с параллельной связью предложений 5 вопросов
- Тест на тему Литературный язык: понятие, признаки, формы 5 вопросов
- Тест на тему Функции и роль языка в жизни человека и общества 5 вопросов
- Тест на тему Сообщение на тему: «Традиции русской речевой манеры общения» 5 вопросов
- Тест на тему Определение и виды простых осложненных предложений 5 вопросов
- Тест на тему Какие бывают виды текстов? 5 вопросов
- Тест на тему Образование и правописание страдательных причастий настоящего времени 5 вопросов
- Тест на тему Как определить начальную форму прилагательного? 5 вопросов
- Тест на тему Местоимение-прилагательное в русском языке 5 вопросов
- Тест на тему Сборник правил по русскому языку для 6 класса 7 вопросов
- Тест на тему Сборник правил по русскому языку за 5 класс 7 вопросов
- Тест на тему Упражнения для тренировки школьников 7 класса по причастному обороту 9 вопросов
- Тест на тему Тест: Склонение фамилий в русском языке 7 вопросов
- Тест на тему Общеупотребительные и необщеупотребительные слова 5 вопросов
- Тест на тему Дефисное и слитное написание сложных прилагательных 5 вопросов
- Тест на тему Морфологический разбор числительного - правило и примеры 5 вопросов
- Тест на тему Урало-сибирская роспись: истоки, техника, развитие 10 вопросов
- Тест на тему История палехской росписи: зарождение, мастера и художественный стиль 10 вопросов
- Тест на тему История мезенской росписи: происхождение, развитие и символика 10 вопросов
- Тест на тему История жостовской росписи: происхождение, развитие и канон 10 вопросов
- Тест на тему Проект на тему: “Экономика родного края: Самарская область” 5 вопросов
- Тест на тему Как люди узнают о том, что было в прошлом? 5 вопросов
- Тест на тему Какие животные впадают в спячку зимой: объяснения зоологов 7 вопросов
- Тест на тему Сообщение по окружающему миру для 4 класса об острове Врангеля 5 вопросов
- Тест на тему Сообщение о морских обитателях - описание, виды и названия 7 вопросов
- Тест на тему "Банты" - как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Конечно же» - выделяется ли слово запятыми? 5 вопросов
- Тест на тему «Подчеркивать» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Лифты» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Строку» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Апостроф» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Зубчатый» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Прозорлива» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Балашиха» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Реку» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Полно» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Говорено» – как правильно ставить ударение в слове? 5 вопросов
- Тест на тему «Досыта» – как правильно ставить ударение в слове? 5 вопросов