Площадь треугольника - формулы и примеры вычислений

Виды многоугольника

Треугольник — это геометрическая фигура, состоящая из трёх отрезков, соединённых между собой в трёх точках, не принадлежащих одной линии. Эти точки называют вершинами фигуры, а линии — сторонами. Плоскость, заключённая внутри треугольника, является его площадью. Так как стороны образуют угол, то фигуру относят к многоугольнику, в частности, имеющему три угла.

Вершины в математике принято обозначать заглавными буквами A, B, C, а стороны — прописными в соответствии с противолежащими им углами. Углы подписывают буквами греческого алфавита: α, β, и γ. Согласно евклидовой геометрии, сумма углов в фигуре равняется 180 градусам. Поэтому как минимум два угла не должны превышать 90 градусов.

Существуют следующие виды треугольников:

1. Правильный. Фигура, у которой все стороны равны. По-другому его называют равносторонний. Для такого треугольника характерно то, что все углы в нём равны 60 градусам, а центры окружностей вписанного типа и описанного совпадают.
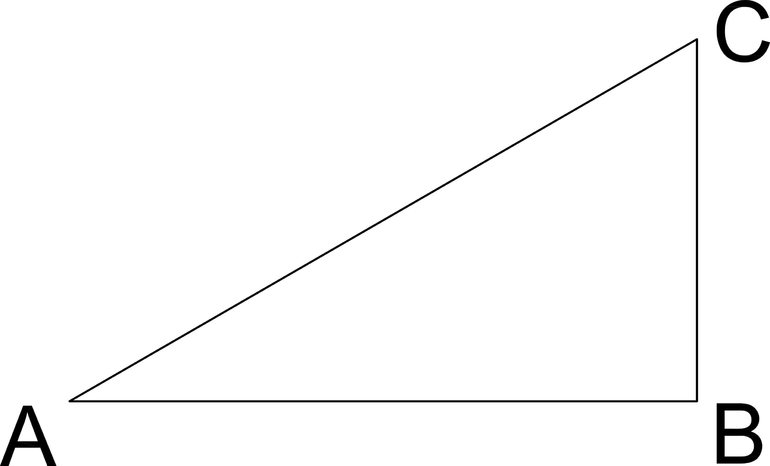
2. Прямоугольный. Треугольник, у которого один из углов составляет 90 градусов. При этом два отрезка, образующих этот угол, называются катетами, а оставшийся — гипотенузой.
3. Тупоугольный. Характеризуется тем, что любой из его углов может быть больше 90 градусов.
4. Равнобедренный. В этом случае две стороны фигуры должны быть равны. Одинаковые грани называют боковыми, а отличную от них — основанием.
5. Разносторонний. Это треугольник, у которого все стороны различны.

Существуют также важные понятия, без знания определений которых невозможно будет выполнить расчёт характеристики. Отрезок, который соединяет вершину с серединой противоположного ей основания, называют медианой. Если провести все возможные медианы в фигуре, а их количество не может быть более трёх, то они пересекутся в одной точке. Место пересечения называется центроидом и является центром тяжести.

Проведённую перпендикулярную линию из вершины на противоположную сторону называют высотой. Точка пересечения трёх возможных высот носит имя ортоцентр. Если же прямая, выходящая из угла, разделяет его на две равные части, то её называют биссектрисой.

Описанная и вписанная окружность

Нахождение площади треугольника связано с такими понятиями, как описанная и вписанная окружность. В формулах для вычисления используется радиус проведённого круга. Самой большой окружностью, находящейся внутри треугольника, является та, что соприкасается со всеми его сторонами. Её центр совпадает с местом пересечения биссектрис.

Вне зависимости от типа треугольника возле него можно начертить три вневписанных окружности. Ими будут круги, которые соприкасаются лишь только с одной стороной фигуры. Изобразив такой круг возле треугольника, можно заметить, что его центр совпадает с пересечением биссектрисы рядом лежащего внутреннего угла и двух других противоположных.

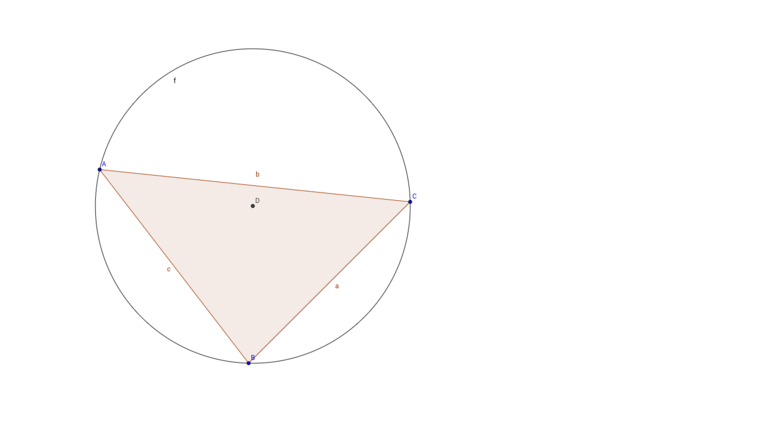
Рассчитать площадь фигуры возможно, используя значения радиусов вписанного и вневписанного круга. Например, пусть имеется произвольный треугольник ABC с вписанной окружностью. Если его радиус обозначить как R, а центр — K, то радиус угла С будет являться высотой KAB. Таким образом, это высота определяется основанием отрезка С и высотой R. Исходя из этого, площадь будет определяться выражением: S1 = C*R/2.

По такому же принципу можно найти площади двух оставшихся треугольников. Один из них будет равен S2 = BR/2, а другой S2 = AR/2. Так как эти треугольники образуют ABC, то сложением S1, S2, S3 может быть найдена общая площадь: S = (A + B + C) * R /2 = p * R, где p — полупериметр.

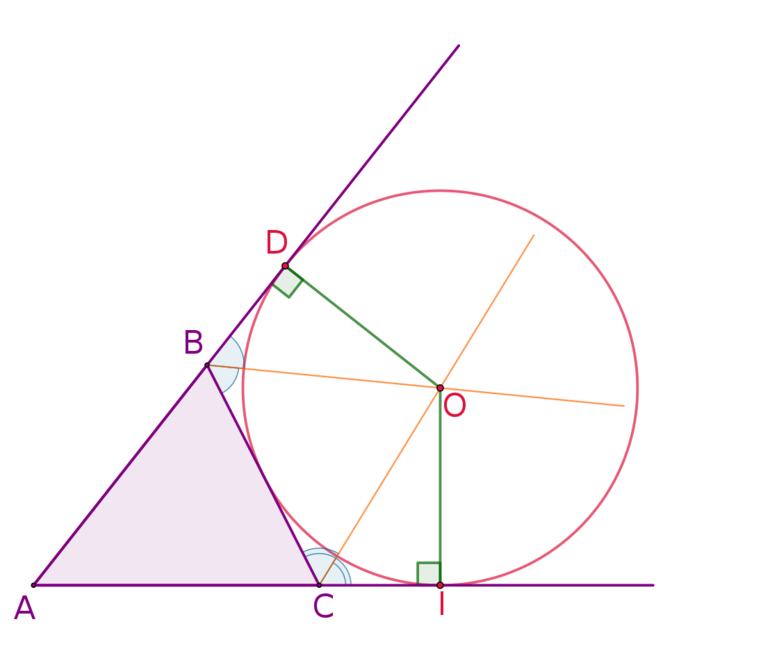
Вневписанные окружности являются продолжением сторон. Если такой круг касается отрезка АВ, то он будет касаться продолжения стороны АС в точке T. Пусть его радиус равен Rc, а центр — Kc. В этом случае Kc * T будет высотой фигуры ACKc. Площадь каждого из трёх треугольников определяется как половина произведения значений стороны на радиус.

Исходя из этого, общую площадь находят из выражения: So = s*R = (p — A) * Ra = (p — B) * Rb = (p — C) * Rc. Используя теорему косинусов и тождество sin²x + cos²x = 1, формулу для нахождения площади можно представить, как Sо = b * c * sinA = (p (p — a) * (p — b) * (p — c))^½.

Полученная формула носит имя математика Герона, изучавшего свойства целочисленных треугольников. С её помощью можно выполнить расчёт площади, зная только три стороны фигуры.

Классический расчёт

С решением задачи по нахождению площади правильного треугольника, впрочем, как и любого другого, знакомят в восьмом классе средней школы на уроках геометрии. Для того чтобы учащиеся поняли идею нахождения площади, используют доказательства, с помощью которых подтверждаются используемые формулы.

Классическая формула для расчёта треугольника равна произведению сторон на синус угла, лежащего между этими отрезками. Для доказательства можно рассмотреть произвольную фигуру, например, равносторонний треугольник. Площадь его согласно теореме равна: S = (½)*BC*CA*sin с. Чтобы утверждать о справедливости этого выражения, необходимо выполнить следующее:

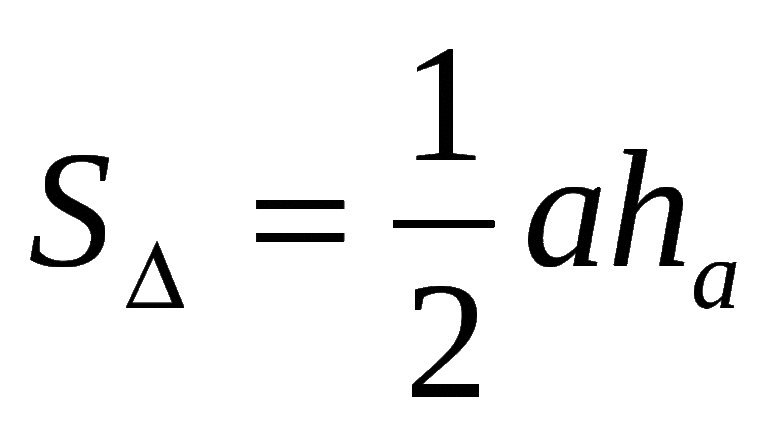
1. Ввести систему координат с начальной точкой С.
2. Расположить её так, чтобы точка B располагалась в плюсовом направлении оси Сx, а A имела положительное значение.
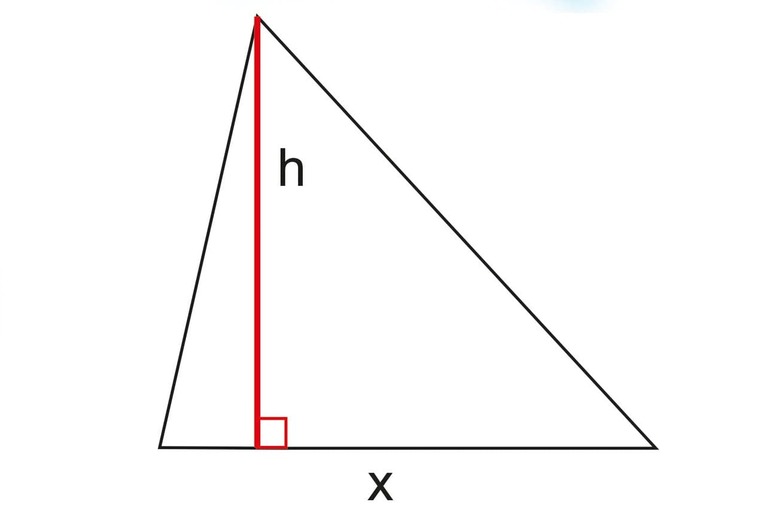
3. Так как площадь фигуры находится из выражения S = a * h /2, где h — высота, то справедливо будет утверждать, что она ордината точки A. То есть h = b*sin с.
4. Учитывая полученное, формулу можно переписать как S = (½)*a*b*sin с.

Например, нужно найти площадь фигуры, у которой одна сторона равна 14 см, вторая 7 см, а угол между ними 48 градусов. Подставив известные значения в рассмотренную формулу, несложно найти ответ: S = (CA*CB*sinс)/2 = (14*7*sin48˚ см²) /2 = 35 см².

На практике приходится сталкиваться и с обратными задачами. То есть когда дана площадь, а найти необходимо одну из сторон. Пусть площадь ABC равна 120 см². Требуется определить сторону AB, если AC = 30 см, а угол α равен 30 градусам. Используя формулу для нахождения площади, можно записать равенство: 120 = (AB*30*sin30˚)/2 = 30*AB /4. Выразив искомую сторону, будет найден ответ: AB = (120*4)/30 = 16 см.

Прямоугольный треугольник

Площадь в таком типе фигуры находится как произведение катетов, делённое пополам: S = AC*BC/2. Если в треугольнике известна гипотенуза или катет, можно воспользоваться следующей формулой: S = AB2 * sin (2 α)/4 или через тангенс S = BC2 * tg β/2. Аналогичные формулы можно использовать и со вторым катетом.

При вычислении площади прямоугольного треугольника целесообразно использовать теорему Пифагора. Она устанавливает зависимость между сторонами фигуры и гипотенузой. Впервые о такой зависимости высказался Евклид, а после Пифагор смог доказать выдвинутое им предположение. Согласно правилу, квадрат стороны, расположенный напротив прямого угла, находится как сумма квадратов сторон, образующих этот угол.

Доказывается это утверждение следующим образом. Пусть задан прямоугольный треугольник ABC, у которого угол C — прямой. Начертив высоту h на гипотенузу, основание обозначим K. Получившиеся два треугольника подобны по углам ACB и CKA. Равняются они 90 градусам. Аналогично CBK подобен ABC. Используя свойство подобных треугольников, верно будет записать: BC / AB = KB / BC и AC / AB = AK / AC. После упрощения подобия получится: BC² = AB * KB, AC² = AB * AK.

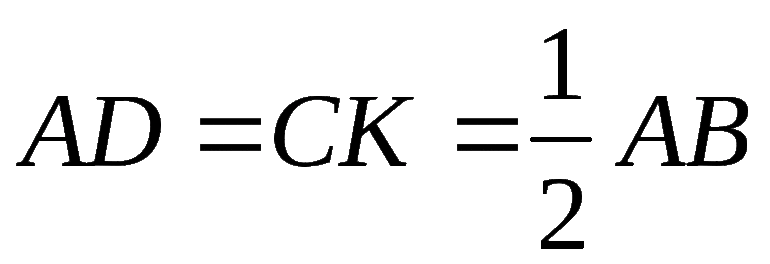
Затем необходимо сложить найденные уравнения: BC² + AC² = AB * KB + AB * AK. Левую часть можно упростить до вида: BC² + AC² = AB * (KB + AK). Сумма сторон в скобках равняется AB. В итоге уравнение примет вид: BC² + AC² = AB², что и необходимо было доказать.

Например, пусть дано, что гипотенуза в прямоугольном треугольнике равна 50 см. При этом размер одного из катетов превышает другой на 10 см. Необходимо найти площадь. Если обозначить одну из неизвестных сторон как x, то вторая будет равняться x+10. Используя теорему Пифагора, можно записать: X² + (x+10)² = 50².

Раскрыв скобки и сведя подобные, уравнение можно привести к виду: x2 + 10x — 600 = 0. Решением этого равенства будут корни 15 и -20. Отрицательный ответ не может удовлетворять условию задачи, поэтому второй катет равняется 15 см. Используя правило нахождения площади, можно найти ответ на задачу: S = 15*20/2 = 150 см².

Равнобедренная фигура

Её частным вариантом является правильный треугольник. Основным признаком такого типа фигуры является то, что углы при основании равны, а также биссектриса, медиана и высота совпадают. Кроме принятого метода нахождения площади равнобедренного треугольника S = b * h /2, где b — основание, а h — высота, решить задачу можно, используя отношение Герона:

S = BC /4* (4* AB ² — AC ² )^½.

Для доказательства приведённой формулы используют теорему Пифагора. Если из угла γ опустить высоту, то получится два остроугольника с основаниями l и k- l. Для двух гипотенуз выражения: BC² = h² + (AC² — l) и AB² = h² + (AC² — l²). Отняв второе уравнение из первого, получится равенство: BC² — AB² = AC² — 2* AC * I. Если выразить основание первого прямоугольника через стороны, то будет верно:

I = (-BC² + AB² + AC²) /2*AC.

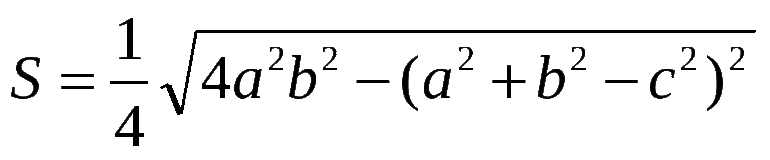
Для высоты h² = AB² — I², подставив найденное выражение и применив формулу квадратов, получим следующее: h² = AB² — ((-BC² + AB² + AC²) /2*AC)^½ = (AB2 + AC — BC) * (AB2 + AC + BC) * (BC + AB — AC) * (BC + AB — AC) /4*AC². Учитывая, что AB + AC — BC = 2*p — 2*BC, BC + AB +AC = 2*p, BC + AB — AC = 2p-2AC, BC + AB — AC = 2p — 2AB, получится: h² = 4p* (p — BC) * (p — AB) * (p-AC) /AC².

Взяв за основу равенство S = AC*h/2 и заменив в нём высоту выведенным выражением, можно записать: S = BC/4* (4*AB² — AC²)^½, что и требовалось доказать.

Рассмотрим пример. Пусть дан остроугольный треугольник с основанием, равным три сантиметра, и одной из сторон шесть сантиметров. Для нахождения ответа подставив исходные данные в формулу, получим: S = 3 * ¼ * (4 * 62 — 32)½ = (144 — 9)½ = 8,7 см². Найти можно, и используя формулу: S = α2 * sin β. В этом случае для перевода величины угла из градусов в количественное значение используют таблицу синусов.

Вычисление онлайн

Провести вычисления, зная формулы, обычно не составляет трудностей. Но порой приходится работать с нецелыми числами, содержащими тысячные коэффициенты. Допустить при этом ошибку довольно легко. Поэтому и существуют так называемые онлайн-калькуляторы, быстро и точно рассчитывающие ответ.

Для того чтобы воспользоваться ими, пользователю даже не нужно знать формулы и методику решений. Всё, что требуется, это точные исходные данные и доступ к сайту. В интернете существует несколько десятков сервисов, предлагающих такого рода услуги бесплатно. Из наиболее популярных можно выделить:

1. «МногоФормул». Сайт предлагает рассчитать площадь треугольника всеми возможными методами на выбор. Все вычисления сопровождаются подробным описанием с иллюстрациями.
2. OnlineMSchool. Используя этот ресурс, пользователь сможет получить детальное пошаговое решение для введённого им примера. Это позволит не только получить правильный ответ, но и разобраться в алгоритме.
3. Allcalc. Кроме непосредственного решения задачи по нахождению площади интернет-портал содержит всю необходимую теорию, используемую для проведения расчётов.
4. «Мозган». Интуитивно понятный интерфейс сайта даёт возможность за несколько секунд получить точный ответ для заданий различной сложности.

Эти сайты можно использовать не только новичкам, пытающимся разобраться в премудростях вычисления, но также и опытным математикам для проверки своих расчётов или просто экономии времени.

​